|
Экспертные оценки
часто возникают на практике, например, при дегустации продуктов питания.
Вообще они типичны для социологических опросов, например, менеджер
по контролю качества проводит опрос покупателей в супермаркете. При
использовании экспертного метода для оценки качества часто используется
шкала порядка. Решается вопрос сравнеия по принципу лучше хуже,
больше меньше. Более подробная информация о том, во сколько
раз лучше или хуже часто не требуется.
Попарное сравнение
(объекты сравниваются друг с другом попарно). При построении шкалы
порядка или так называемого ранжированного ряда эксперты используют
метод попарного сопоставления. В таб. 1 приведен
пример ранжирования шести объектов путем попарного сравнения. Это
результат работы одного эксперта, оценивавшего объекты определенным
образом. Предпочтение одного объекта перед другим обозначено 1, обратная
ситуация - 0.
Ранжированный
ряд (шкала порядка) для объектов, сравнительная оценка которых
приведена в таб. 1, будет иметь вид:
Q4<Q5<Q6<Q2=Q1<Q3.
Если использовать несколько экспертов, то можно получить более точный
результат.
Можно использовать более совершенные критерии, например, преимущество
определить оценкой 1, худшее качество определить оценкой -1, а равноценное
качество определить оценкой 0. Механизм составления ранжированного ряда
остается прежним.
Психологами доказано, что попарное сопоставление лежит в основе любого
выбора (т.е. Вы выбираете продукты, сравнивая их попарно), тем не менее,
шкалу порядка часто составляют заранее ( не ранжированный ряд) и фиксируют
в ней опорные (реперные) точки, которые называют баллами.
Так появилась двенадцатибальная
шкала интенсивности землетрясений MSK - 64, минералогическая шкала
Мооса, пятибалльная шкала оценки знаний, баллы в фигурном катании
и т.д. В таблице 2 в качестве примера приведена шкала твердости минералов
Мооса.
Таблица
1. Ранжирование шести объектов путем попарного сравнения
Таблица
2. Шкала Мооса
Каждый
последующий минерал оставляет царапину на предыдущем, т.е. является
более твердым. Результаты измерений, полученные попарным сопоставлением,
можно уточнить методом последовательного приближения.
Влияние состава
экспертов на результаты экспертизы
При формировании
экспертной группы целесообразно провести тестирование, взаимооценку
экспертов и проверку согласованности мнений.
Тестирование
состоит в решении экспертами задач, с известными организаторам тестирования,
но неизвестными экспертам результатами, и проверке по критерию Фишера
гипотезы о принадлежности оценок разных экспертов к одной и той же
генеральной совокупности оценок.
Самооценка состоит
в том, что каждый эксперт в ограниченное время отвечает на вопросы
специально составленной анкеты. Такое испытание проводят на компьютере
и затем получают балльную оценку. Эксперты могут оценивать и друг
друга, но для этого необходима доверительная обстановка и опыт совместной
работы. Согласованность мнения экспертов можно оценивать по величине
коэффициента конкордации:
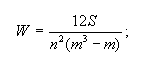
где S -
сумма квадратов отклонений всех оценок рангов каждого объекта экспертизы
от среднего значения;
n - число экспертов;
m - число объектов экспертизы.
Коэффициент конкордации
изменяется в диапазоне 0<W<1, причем 0 - полная несогласованность,
1 - полное единодушие.
Пример
Необходимо
определить степень согласованности мнения пяти экспертов, результаты
ранжирования которыми семи объектов приведены в таблице 3. Для определения
степени согласованности используется специальная мера - (от лат. concordare - привести в соответствие,
упорядочить).
| Номер
объекта экспертизы |
Оценка
эксперта |
Сумма
рангов |
Отклонение
от среднего |
Квадрат
отклонения |
| 1 |
2 |
3 |
4 |
5 |
| 1 |
4 |
6 |
4 |
4 |
3 |
21 |
1 |
1 |
| 2 |
3 |
3 |
2 |
3 |
4 |
15 |
-5 |
25 |
| 3 |
2 |
2 |
1 |
2 |
2 |
9 |
11 |
121 |
| 4 |
6 |
5 |
6 |
5 |
6 |
28 |
8 |
64 |
| 5 |
1 |
1 |
3 |
1 |
1 |
7 |
-13 |
169 |
| 6 |
5 |
4 |
5 |
6 |
5 |
25 |
5 |
25 |
| 7 |
7 |
7 |
7 |
7 |
7 |
35 |
15 |
225 |
Таблица
3. Данные для оценки согласованности мнений пяти экспертов
Оцениваем
среднеарифметическое число рангов:
Qср
= (21 + 15 + 9 + 28 + 7 + 25 + 35)/7 = 20.
Затем
оцениваем сумму квадратов отклонений от среднего: S = 630. Определяем
величину коэффициента конкордации:
W
= 12 * 630 / 25 * (343 - 7) = 0,9.
Много
это или мало? Если провести соответствующие вычисления в ,
то можно получить следующую таблицу результатов:
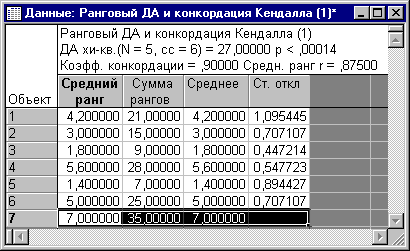
Рис. 1. Результаты проведения анализа в
STATISTICA.
Из
этой таблицы следует, что различные мнения экспертов в данном примере
незначимы: р<0.00014.
Влияние
на результаты экспертизы количественного состава экспертов. С ростом
числа экспертов в группе точность измерения повышается, что характерно
для многократных измерений.
Количество
экспертов n, обеспечивающее заданную точность измерений, можно
установить, зная закон распределения мнений экспертов и максимально
допустимую стандартную ошибку оценки Sx. Тогда,
используя известное выражение, можно определить минимальное количесвто
экспертов n, обеспечивающее заданную точность измерения:
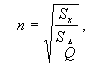
где
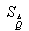 -
, которое определяют по формуле: -
, которое определяют по формуле:
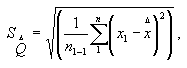
где
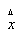 -
среднеарифметическое значение оценок экспертов; -
среднеарифметическое значение оценок экспертов;
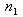 -
число оценок, дававшихся экспертами. -
число оценок, дававшихся экспертами.
Различают
также индивидуальное и коллективное мнение экспертов, последнее считают
более точным, а главное, согласованным. В роли экспертов могут выступать
люди со специальной подготовкой, потенциальные потребители и изготовители
продукции.

| 
