| Напомним,
что в соответствии с положениями теоретической метрологии измерение
может выполняться с использованием шкалы порядка (уровней), шкалы
интервалов и шкалы отношений.
Во
втором и третьем случаях результат измерения является случайной величиной
и может записываться выражением:

где
X - показание средства измерения;
 -
поправка. -
поправка.
Величина
Х характеризует правильность показаний, а поправка - точность
измерений. По этим параметрам измерительная техника разделяется на
классы точности в соответствии с допускаемой погрешностью измерений.
Приведенная
погрешность измеряется в процентах от верхнего предела измерений,
относительная погрешность - то результата самого показания.
Используется
ряд классов точности, в том числе: 0.1, 0.2, 0.5, 1.0, 1.5, 2.5, 4.0.
Характеристикой класса является относительная погрешность, указываемая
в процентах: 0.1, 0.5, 4.0.
Правильность
результата измерения обеспечивается совпадением среднего значения
измерений со значением измеряемой величины.
Значение
Х - величина случайная, поправка не является случайной, она
характеризует относительную погрешность измерения.
На
рис. 1 показано распределение плотности вероятности при точных измерениях
(1) и менее точных (2).
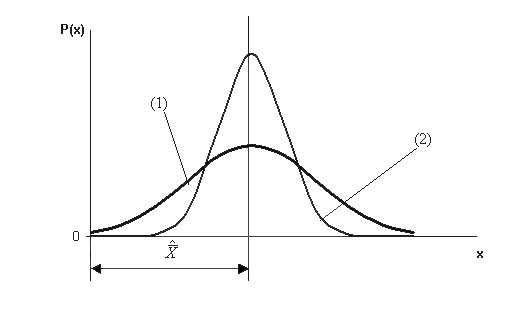
Рис.1 Распределение плотности вероятности при двух классах точности
измерений
Если
значение поправки с течением времени не меняется, то при многократном
измерении постоянного размера одним и тем же средством измерений (в
одинаковых условиях) получим:
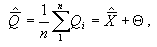
где
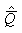 -
средний арифметический результат измерений; -
средний арифметический результат измерений;
n - количество измерений;
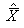 -
среднее значение показания при измерении; -
среднее значение показания при измерении;
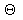 -
значение поправки; -
значение поправки;
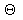 =const. =const.
Это
выражение показывает, что точность многократного измерения выше, но
правильность такая же, как и при однократном измерении.
Пример
1. При метрологической аттестации вольтметра в нормальных условиях
выполнено 100 измерений образцового напряжения в различных точках
шкалы. Установлено, что распределение вероятности с дисперсией 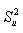 напряжение равно 1,5В.
напряжение равно 1,5В. Смещение среднеарифметического значения в сторону меньших значений
с вероятностью 0,95 достигает 0,3В. Необходимо сравнить качество однократных
и многократных измерений.
Смещение среднеарифметического значения в сторону меньших значений
с вероятностью 0,95 достигает 0,3В. Необходимо сравнить качество однократных
и многократных измерений.
Решение.
Из результатов аттестации следует, что в показания вольтметра нужно
вносить поправку =+0,3В.
Стандартная
ошибка (среднеквадратическое отклонение) составляет:
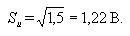
Если
показания вольтметра U = 20В, то результат измерения можно
записать в виде:
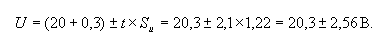
Результат
измерения: U = 17,74 ... 22,86 В
Точность
многократного измерения выше, и соответствующие показатели качества
измерения при девяти отсчетах составят:
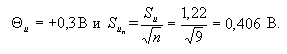
Допустим,
вольтметр дал девять показаний: 20; 21; 20,5; 21; 20,5; 21,5; 20,5;
20,5; 21,2. Тогда 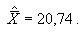
Результат
измерения можно записать следующим образом:
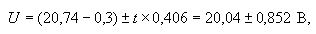
U = 20,188
... 21,892.
Погрешность
составляет 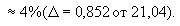
При
обдновременном измерении одного и того же размера (параметра) разными
средствами нужно верно квалифицировать исходную информацию.
Допустим,
что точность и правильность однократных измерений отдельными средствами
измерений известны, но в паспортных данных приборов приводится значение
поправки, которую нужно ввести в показание. Результат измерения 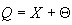 можно рассматривать как сумму двух случайных величин:
можно рассматривать как сумму двух случайных величин:
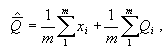
где
m - число измерений.
Если
X и  подчиняется
нормальному закону распределения, то точность и правильность определяют
с использованием формул: подчиняется
нормальному закону распределения, то точность и правильность определяют
с использованием формул:
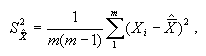
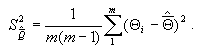
В
рассматриваемом случае поправка рассматривается как случайная величина.
Такая процедура называется рандомизацией. Приведенные
формулы показывают, что рандомизация результата измерения одного и
того же параметра улучшается и по точности и по правильности.
Пример
2. В табл. 1 приведены числовые значения 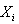 одиннадцати
измерений одного и того же параметра разными средствами измерений.
Даны поправки одиннадцати
измерений одного и того же параметра разными средствами измерений.
Даны поправки 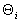 ,
заимствованные из паспортных данных. Вычислим средние значения измеренного
параметра и поправок приборов: ,
заимствованные из паспортных данных. Вычислим средние значения измеренного
параметра и поправок приборов:
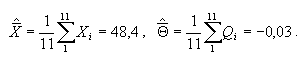
После
этого определим, в каких пределах находится измеряемое значение и
каковы показатели качества результата измерения.
| Номер
прибора |
Xi |
Qi |
| 1 |
48,3 |
0,3 |
| 2 |
48,5 |
-0,1 |
| 3 |
48,2 |
0 |
| 4 |
48,5 |
-0,5 |
| 5 |
48,4 |
0,2 |
| 6 |
48,6 |
-0,3 |
| 7 |
48,5 |
0,1 |
| 8 |
48,4 |
0 |
| 9 |
48,6 |
-0,4 |
| 10 |
48,0 |
0,5 |
| 11 |
48,4 |
-0,1 |
Таблица
1. Результаты измерений одного и того же параметра
Решение.
1.
Среднее значение показания и поправки:
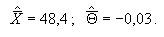
2.
Определим дисперсию 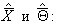
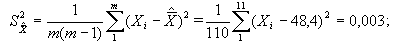
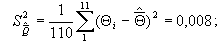
3.
Результат измерения:
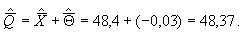
4.
Дисперсия результата измерения:
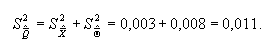
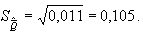
5.
С вероятностью, равной 0,95, можно утверждать, что значение (результат)
не отличается от результата измерения больше, чем на 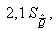 поэтому измеряемое значение:
поэтому измеряемое значение:
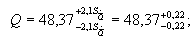
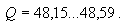
Погрешность 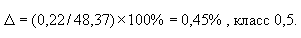

|

