Эмпирическая функция распределения и гистограмма результатов испытаний

В данном изложении рассматриваются общие методы получения оценок параметров, определяющих надежность изделий.

Эти методы могут быть использованы при обработке результатов наблюдений над изделием, срок безотказной работы которых подчинен тому или иному распределению - , , логарифмически нормальному и др. (эти распределения реализованы в ).

Чисто технически трудности заставляют нас ограничиться только планами [N, Б, r] и [N, Б, T]. Естественно, что последующие результаты применимы при обработке результатов не только элементов, но и сложных систем и машин (например, космических кораблей, комбайнов, сложной техники).

План [N, Б, N]

Напомним, что план [N, Б, N] означает испытание N элементов до отказа последнего элемента; отказавшие элементы не заменяются новыми.

План [N, Б, N] можно использовать или в случае, когда элементы сравнительно ненадежны, или же при проведении ускоренных испытаний.

Предположим, что испытываемые элементы занумерованы числами 1, …, N и i-й элемент отказывает в момент . Первый отказ наступает в момент , где - номер элемента, оказавшего первым; - случайное число. Второй отказ наступает в момент и т.д. Наконец, в момент отказывает последний элемент.

В статистике так упорядоченную последовательность чисел называют вариационным рядом или порядковыми статистиками для наблюдений .

При использовании [N, Б, T] наблюдаются только те отказы, которые происходят до момента времени Т. Если - последовательные моменты отказов, то, в результате испытаний мы наблюдаем случайное число отказов, происходящих в моменты (Отказ с номером , если он возможен, наступает после момента Т).

Таким образом, означает номер последнего отказа, который происходит до момента Т окончания испытаний. Если элементы достаточно надежно работают в интервале времени (0, Т), то нередко случается, что отказы не наблюдаются и =0. Заметим теперь же, что отсутствие отказов во время испытаний, т.е. условие =0, не дает нам право заключить, что надежность изделий равна 1.

Наиболее полной характеристикой надежности элементов является функция распределения F(t) времени безотказной работы. О виде функции распределения можно судить по так называемой эмпирической функции распределения, определяемой посредством равенства для значений х, . Согласно теореме Гливенко с вероятностью 1 .

Рис.1. Эмпирические функции распределения и .

На рисунке показаны эмпирические функции распределения и , когда теоретическая функция распределения . Если используется план [N, Б, T], то значения эмпирической функции могут быть определены только для . Если же используется план [N, Б, r], то значения эмпирической функции определяются только до уровня .

Оценкой плотности вероятностей может служить так называемая гистограмма .

В отличие от эмпирической функции гистограмма может быть построена различными способами. Например, можно разбить область значений времени t на интервалы и на каждом из этих интервалов положить

где - число отказов, которые наблюдались в интервале .

Рис.2. Гистограмма для показательного закона F(t)

На рис. 2, а приведен пример построения гистограммы для показательного закона

При втором способе выбирается число интервалов , так что , при этом , а остаток от деления также близок к Первый интервал - , где совпадает с моментом отказа, второй интервал - совпадает с моментом отказа и т.д., наконец, k-й интервал -

Последний, (k+1)-й, интервал - На каждом из k интервалов группировки , полагаем

на интервале Гистограмма, построенная по этому способу для

Функция опасности отказов определяется по формуле

Если число испытываемых элементов N велико и интервалы между последовательными моментами отказов сравнительно невелики, то можно построить эмпирическую функцию опасности отказов. Ось времени разбиваем на несколько участков

Оценкой для является отношение - случайная величина. За оценку для берем - число элементов, отказавших на интервале Эмпирическую функцию опасности отказов полагаем равной отношению При этом интервалы можно выбирать способом, аналогичным одному из описанных выше способов построения гистограммы.

Иногда не обязательно знать всю функцию распределения , ее плотность или ее функцию отказов , а достаточно знать лишь некоторые характеристики: моменты, квартили и др. Момент k - го порядка в случае плана [N, Б, N] определяется по формуле

центральный момент порядка - по формуле

Число такое, что , называется квантилью уровня р.

Эмпирической квантилью уровня р называется одно из решений уравнения . Мы всюду предполагаем, что является непрерывной.

Три типа статистической устойчивости

В случае плана [N, Б, N] нам известна вся эмпирическая функция распределения , а в случае плана [N, Б, T] - лишь часть ее определенная для значений . Для оценки неизвестной функции распределения и различных числовых ее характеристик возможны три принципиально различных подхода, соответствующих различным реальным условиям, в которых решается задача.

В первом, наиболее простом случае заранее известен тип закона распределения . Например, в результате теоретических исследований и последующей экспериментальной проверки показано, что для определенного типа элементов и аппаратуры закон распределения времени безотказной работы является показательным, т.е. Неизвестно лишь значение параметра которое надо оценить по результатам проведенных испытаний.

Во втором случае не теоретических соображений, из которых следовало бы, что тип закона распределения должен быть вполне определенным, например, показательным, логарифмически нормальным или каким-то другим. Однако результаты испытаний показывают, что эмпирические функции распределения могут быть приближены плавно меняющимися функциями распределений.

Из предварительной обработки экспериментальных данных видно, что качественный характер поведения эмпирических функций распределения или гистограмм не меняется от партии к партии.
Пусть гистограммы имеют существенную асимметрию и одновершинны.
В таких случаях подбирают одно из возможных семейств функций распределения, или плотностей, для которого качественное поведение функций распределения, или плотностей, соответствует полученным экспериментальным данным.
Если семейство распределений выбрано, то задача определения функции и ее характеристик сводится к оценке по результатам испытания неизвестных значений параметров или функций от них.

Например, если мы пытаемся приближенно описать данные с помощью логарифмически нормального закона, то неизвестными значениями параметров являются При этом в самом начале работ полезно сравнить результаты, получаемые при использовании двух-трех типов семейств распределений. Если два семейства дают одинаково хорошие результаты, то для дальнейшего использования выбирается то из них, для которого можно предложить теоретические обоснования. В том же случае, когда теоретических предпосылок для выбора распределения нет, нужно предпочесть то, для которого трудоемкость числовых расчетов меньше.

Возможен, однако, и третий случай условий производства, когда качественный характер эмпирической функции меняется от партии к партии или же когда для приближений нужны семейства со многими неизвестными параметрами и соответственно требуются громоздкие вычисления необходимых характеристик. В этих случаях можно использовать некоторые методы непараметрической статистики, т.е. методы, не связанные с аналитическим видом функции распределения .

Для весьма надежных элементов реализация плана [N, Б, N] или [N, B, N] приводит к необходимости проведения испытаний в течение многих тысяч часов. Именно по этой причине часто используются различные планы с фиксированной длительностью испытаний ([N, Б, T], [N, B, T], [N, Б, (r, T)], [N, B, (r, T)] и др.).

При этом по наблюдениям, полученным за ограниченный промежуток времени, нужно оценить различные показатели надежности, связанные с отказами, которые могут произойти после момента Т, среднее время безотказной работы в течение времени и др. Использование результатов за ограниченное время наблюдения для получения оценок всевозможных характеристик надежности законно в первом случае, когда вид функции распределения нам известен до опыта и только неизвестны значения параметров, определяющих этот закон.

Во втором случае надо иметь достаточный статистический материал, который хотя бы косвенно подтверждал правильность выводимых числовых оценок. Таким косвенным подтверждением могут служить результаты испытаний отдельных партий элементов, проводившихся в течение длительного времени, или сведений об отказах эксплуатируемого оборудования.

Наконец, в третьем случае, когда нет устойчивости даже качественного поведения эмпирической функции распределения, получения оценок любых характеристик надежности, которые определяются по значениям для t>T, где Т - время испытаний, не является законным. В этом случае, прежде всего, необходимо отладить технологический процесс.

В подтверждение этих соображений рассмотрим следующий пример. В нем мы намеренно сгустили краски. Предположим, что проводятся испытания элементов N=100. Каждый элемент состоит из двух частей, отказ каждой из которых приводит к отказу элемента (например, проводящий слой сопротивления и контакты). Отказы обеих частей происходят независимо друг от друга.

Таким образом, если - момент, когда произойдет отказ первой части (обрыв), а - момент отказа второй части (уход параметра за пределы допуска), то считается, что отказ элемента произойдет в момент . Предположим далее, что

Однако экспериментатору неизвестно, что закон распределения времени безотказной работы

Вид функции показан на рис. 3.

Рис.3. График функции F(t)

Было решено проводить испытания в течение Т=500 час. Вероятность отказа первого элемента равна

Таким образом, мы в среднем наблюдаем число отказов NF(T) приблизительно равным 100, причем практически все наблюдаемые отказы будут только первого типа (обрыв), так как отказы второго типа (уход параметров) при сделанных выше предположениях начнут наступать после 800 час работы, но зато уже к 1200 час работы почти все элементы выйдут из строя вследствие отказов второго типа. Отказов второго типа в течение Т=500 час мы не наблюдаем, поэтому ошибочно считаем, что закон , и по результатам этих испытаний пользуясь методами следующего параграфа, находим оценку для близкую к 2000.

Итак, по результатам испытаний, проводимых в течение Т=500 час, сделан ошибочный вывод относительно характера распределения.

Вывод из этого примера таков. Надо сначала проверить теоретически или экспериментально (а лучше обоими путями), что вид закона и при значениях t, больших времени Т проведения испытаний, не меняется, а уже затем получать оценки для характеристик надежности.

Рассмотрим теперь некоторые общие методы получения оценок параметров распределения времени безотказной работы. При оценке параметров конкретного семейства распределений могут быть употреблены различные методы. В зависимости от используемого метода будут получаться отличающиеся друг от друга оценки неизвестных значений параметров. Необходимо провести сравнение различных методов и для дальнейшего выбрать метод, дающий наилучшие результаты. В тех случаях, когда вычисления приходится выполнять вручную, нужно оценивать метод и с точки зрения трудоемкости вычислений.

Графические методы

Первая и наиболее простая группа методов - графические методы оценки. Они применимы для некоторых семейств , содержащих два неизвестных параметра График функции распределения можно представить в виде совокупности точек (t, p) на плоскости, где . Основная идея графического метода состоит в том, что подбирается такая непрерывная замена координат , что при этом график функции распределения , где , становится прямой линией . Если такую замену переменных удалось отыскать, то на плоскости любая функция распределения этого семейства будет представима в виде прямой или, что то же самое, в виде прямой

... (1)

Используем этот факт для оценки параметров Предположим, что в результате испытаний получены N значений некоторой случайной величины (например, времени безотказной работы элемента или интервалов между отказами в аппаратуре). По этим значениям мы можем построить эмпирическую функцию распределения . Так как эмпирическая функция при больших N лежит вблизи от теоретической функции распределения , то после замены переменных график , а , будет лежать в непосредственной близости от графика , являющегося прямой вида (1). Оценив с помощью линейки тангенс наклона k и свободный член b и приравняв их теоретическим значениям, получаем уравнения

... (2)

из которых находим оценки неизвестных значений параметров

Уместно заметить, что графический метод применим для любого плана [N, Б, T], [N, B, T], [N, Б, (r, T)], [N, B, (r, T)], [N, Б, r], [N, B, r]. Например, в случае плана [N, Б, (r, T)] по результатам испытаний можем построить только часть для значений - число элементов, отказавших за время проведения испытаний. Если к полученному куску эмпирической функции распределения применить преобразования , то на плоскости получим кусок ломаной, близкой к одной из прямых вида (1). ). По этому куску оцениванием k и b и снова приходим к уравнению (2).

Для примера, рассмотрим три семейства распределений. В случае нормального семейства распределений.

в качестве преобразования рассмотрим функцию , обратную к функции . При этом получаем

... (3)

Таким образом, (3) соответствует (2), когда

Для удобства пользования выпускается специальная нормальная вероятностная бумага. По оси абсцисс отложены значения t случайной величины, а по оси ординат - значения функции . При этом ось t проводится через точку 0, соответствующую .

Около каждого значения отмечается соответствующее ему значение р (рис. 4).

Рис.4. Нормальная вероятностная бумага

Функция распределения записывается в виде прямой y=x. Прямой соответствует функция распределения нормальной случайной величины со средним и дисперсией .

Таким образом, с помощью вероятностной бумаги можно легко проверять на глаз нормальность закона распределения, а заодно и оценивать его параметры. Если ломаная имеет заметную искривленность, то это говорит о том, что истинный закон распределения не является нормальным. Если же искривленности нет, то, проводя на глаз прямую, наиболее плотно прилегающую к ломаной, легко находим оценки для и . равно абсциссе точки А, где А - точка пересечения прямой с осью t; равно расстоянию от А до В, где В - точка на оси t, в которой величина перпендикуляра, опущенного из точки прямой на ось t, равна 1 (в единицах масштаба оси абсцисс).

В случаях логарифмически нормального закона , поэтому

Если задано семейство показательных распределений со сдвигом

... (4)

где . Поэтому в качестве выбираем функцию . Сравнивая (4) с (1), видим, что .

Наконец, если нам задано семейство распределений Вейбулла

то

... (5)

Сравнивая (5) с (1), находим, что

Вид бумаги для закона Вейбулла показан на рис. 5.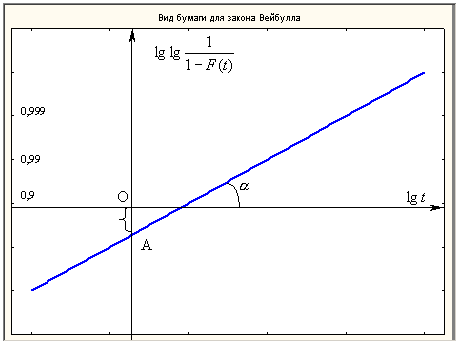

Рис.5. Вид бумаги для закона Вейбулла

Таким образом, тангенс угла наклона равен р, а логарифм равен величине отрезка ОА, отсекаемого прямой на оси ординат.

Методы квантилей и моментов

Для получения оценок неизвестных значений параметров, определяющих вид закона распределения времени безотказной работы, могут быть использованы методы моментов и квантилей. Здесь мы рассматриваем эти методы с точки зрения обработки результатов испытаний, полученных при использовании некоторых планов типа Б. Для определенности мы ограничимся случаем двух неизвестных параметров и .

Пусть закон распределения времени безотказной работы имеет непрерывно дифференцируемую плотность, принимающую положительные значения для любых возможных значений параметров , .

Если испытания проводились по плану [N, Б, r], , то момент появления -го отказа можно рассматривать как эмпирическую квантиль, соответствующую уровню . Если и N достаточно велики, то можно считать, что имеют нормальное распределение с нулевым средним и матрицей дисперсий

где

Если бы значения квантилей , были ним известны точно, то значения параметров , можно было бы найти из уравнений

... (6)

Нам известны, лишь приближенные значения этих квантилей - моменты появления l-го и r-го отказов. Заменяя в уравнениях (6) значения квантилей их оценками, получаем уравнения

... (7)

решения которых являются состоятельными оценками для параметров , при , что непосредственно следует из непрерывности функции . Можно показать, что эти оценки при весьма общих предположениях типа гладкости функции являются асимптотически несмещенными и асимптотически нормально распределенными. Поэтому наиболее существенными показателями качества таких оценок являются их дисперсии.

Проиллюстрируем метод квантилей на примере закона Вейбулла

Испытания проводятся по плану [N, Б, r]. Выбирается значение l (можно выбрать ). В результате испытаний фиксируются значения и моментов l-го и r-го отказов. Уравнения (7) переписываются в виде

Решая их относительно неизвестных значений параметров p, , получаем оценки

Если предположить, что у существуют вторые непрерывные частные производные по t и параметрам , , то, используя обычный прием разложения в ряд Тейлора, можно получить приближенное выражение для дисперсии оценок параметров , .

Введем обозначения

Из уравнений (7) находим

Заметив, что , получаем с точностью до бесконечно малых высших порядков

... (8)
Аналогично находим, что
... (8')

Разрешая эти линейные уравнения (8) и (8') относительно ошибок , получаем их в виде линейных комбинаций от :

Отсюда, используя матрицу вторых моментов для квантелей , можно найти дисперсии ошибок

... (9)

В частности, в случае закона Вейбулла получаем

Метод квантилей в несколько видоизмененной форме можно использовать и в случае планов [N, Б, T]. В этом случае вместо уравнения (6) можем записать

... (10)

где . Однако значения при нам неизвестны. Нам известны лишь числа отказов, происшедших к моментам . При больших значениях N отношения близки к теоретическим значениям . Поэтому, заменяя в (10) значения их оценками, получаем уравнения

... (11)

для нахождения оценок . Используя разложение функции в ряд Тейлора по параметрам и , можно найти приближенные выражения для дисперсий оценок. Если объем выборки N велик, то можно для получения оценки параметров использовать не все данные, а только значения k определенным образом выбранных эмпирических квантилей,

При этом числа подбираются таким образом, чтобы дисперсии ошибок неизвестных параметров были бы минимальными. Например, для случая закона экспоненциального типа оценка ищется в виде линейной комбинации

... (12)

где коэффициенты и числа подобраны таким образом, чтобы дисперсия оценки была наименьшей. Как известно, наилучшей оценкой для параметра при использовании всех данных является . Подсчет отношения дисперсий этих оценок в зависимости от выбранного числа квантилей k показал, что

Так же как и метод квантилей, метод моментов может быть использован только при обработке результатов испытаний, в которых наблюдаемое число отказов достаточно велико. Если испытания проводится в соответствии с планом [N, Б, T], то условная плотность вероятности распределения момента отказа при условии, что такой отказ произошел за время испытаний Т, равна .

Таким образом, для момента k-го порядка, относящегося к наблюдаемым отказам, имеем ... (13)

Если - число зарегистрированных за время Т отказов, а моменты отказов , то эмпирические моменты первого и второго порядков равны

Если достаточно велико, то в силу закона больших чисел значения эмпирических моментов близки к теоретическим. Приравнивая значения теоретических моментов в (13) значениям эмпирических моментов, получаем уравнения для нахождения оценок :

... (14)

Если испытания проводились в соответствии с планом типа [N, Б, r], , то соответствующие уравнения для оценок можно получить, исходя из средних значений для членов вариационного ряда. Здесь имеем

... (15)

Выбирая два порядковых номера , получаем уравнения для нахождения оценок

... (16)

где определяется по формуле (15).

В заключение заметим, что можно также использовать и смешанные методы, когда одно из уравнений для нахождения оценок описывается в соответствии с методом квантилей, а другое - в соответствии с методом моментов. Сравнивание эффективности различных методов можно проводить путем сравнения дисперсий полученных оценок. При этом могут быть применены асимптотические методы, аналогичные методу разложения в ряд Тейлора и последующего использования асимптотической нормальности отклонений. Этим методом были получены выражения (9) для дисперсий оценок в методе квантилей.

В качестве примера, иллюстрирующего метод моментов, рассмотрим оценку параметров и в случае, когда плотность вероятности отказов принадлежит семейству гамма-распределений , а испытания проводились в соответствии с планом [N, Б, N]. Так как ... (17)

а оценками для являются , то, заменяя в (17) моменты оценками, получаем уравнения

Решения этих уравнений имеют вид

... (18)

Введем обозначения и используем метод разложения в ряд Тейлора

... (19)

Символы означают, что рассматриваются значения производных при Заметим теперь, что

... (20)

Из (29) и (20) находим выражения для дисперсий и ковариаций оценок, полученных методом моментов:

Метод максимального правдоподобия

Для оценки параметров наиболее часто используется метод максимального правдоподобия. При ограничениях типа регулярности с помощью метода максимального правдоподобия можно получать асимптотически эффективные оценки. Однако планы типа [N, Б, N] очень редко могут быть использованы при испытаниях весьма надежных элементов, так как их проведение связано с большой длительностью испытаний. В этом случае можно использовать другие планы [N, Б, r], [N, Б, (r, T)] и т.д.

Встает вопрос о том, насколько хороши будут оценки, полученные в результате использования метода максимального правдоподобия для планов, отличных от плана [N, Б, N]. Основная идея получения оценок максимального правдоподобия остается той же.

В случае плана [N, Б, N] множество данных, полученных после проведения испытаний, имело однородную структуру. В результате каждого испытания получаем N чисел , соответствующих моментам отказов. В случае других планов структура множества полученных данных может изменяться от опыта к опыту. Например, может случиться, что при использовании плана [N, Б, (r, T)] за время испытаний Т не произошло ни одного отказа (событие ) или произошло d отказов (событие ), . В случае события множество данных - пустое множество, данных нет; в случае события , , множество данных является наборами d чисел .

Итак, в общем случае мы получаем данные, принадлежащие подмножествам определенного вида, на которых заданы семейства распределений, зависящие от неизвестных значений параметров. Для плана это распределение вероятностей имеет вид: вероятность события , плотность вероятности того, что произошло событие , , и отказы наблюдались в моменты , равна

плотность вероятности того, что произошло событие , и отказы наблюдались в моменты , равна

где . Если результаты испытаний рассматривать как набор случайных чисел, то вероятность или плотность вероятностей исходов испытаний (в нашем примере ) также являются случайными величинами.

Как и в случае плана [N, Б, N] эти случайные величины называют функциями правдоподобия. Для оценки параметров мы подбираем такую пару чисел , что значение функции правдоподобия при фиксированных значениях исходов опыта обращается в максимум. Полученные таким образом оценки называются оценками максимального правдоподобия.

Необходимым условием обращения функции двух переменных в максимум является равенство нулю ее частных производных по и . Если функция не обращается в нуль, то для отыскания точки, где функция обращается в максимум, можно приравнять к нулю частные производные от логарифма этой функции. Для плана [N, Б, (r, T)] и события , , уравнения максимального правдоподобия имеют вид

... (21)

где

Как правило, уравнения (21) являются трансцендентными, и решение их вручную занимает много времени. Однако если испытания с использованием одного и того же плана проводятся систематически, то становится целесообразным использование для вычислений электронных машин. При этом предварительно следует убедиться в существовании решений (21). Если решение этих уравнений не единственно, то необходимо привлечь дополнительные соображения для выбора одного из них.

Для показательного закона распределения уравнение правдоподобия (в случае одного параметра будет одно уравнение), как правило, решается в явном виде.

В заключение заметим, что из явного выражения функции правдоподобия можно сразу выписывать совокупность достаточных статистик, содержащих в себе всю информацию об оцениваемых параметрах. Для этого нужно только воспользоваться критерием факторизации. Применительно к плану [N, Б, (r, T)] из критерия факторизации получаем, что если функция правдоподобия представима в виде

... (22)

где - функции от , а не зависит от и , то статистики являются достаточными для пары параметров . Например, если

то ... (23)

поэтому, полагая и сравнивая (23) с (22), получаем, что статистики являются достаточными для параметров и . В случае достаточными будут статистики К сожалению, достаточные статистики, отличные от полного набора существуют не всегда. В частности, они не существуют для семейства распределений Вейбулла.