|
В задачах
выборочного контроля испрользуются следующие распределения: ,
,
.
Гипергеометрическое распределение возникает в ситуациях, когда имеет
место выбор без возвращения. Структура многомерного гипергеометрического
распределения довольно сложна. При определенных условиях это распределение
аппроксимируется биномиальным распределением. В свою очередь биномиальное
распределение аппроксимируется еще более простым распределением Пуассона.
Итак,
в реальных условиях вместо гипергеометрического распределения (точно
описывающего выбор без возвращения, что имеет место при приемочном
контроле) можно использовать более простое биномиальное распределение
или еще более простое распределение Пуассона. Таким образом можно
получить весьма точные приблежения, достаточные для построения процедуры
контроля. Все эти процедуры реализованы в .
Общая
идея выборочного контроля проста и состоит в следующем.
Решение о качестве партии изделий, принимаемой в результате
выборочного контроля, требует определения объема выборки n при
заданных уровне дефектности q и так называемом браковочном числе
Ас.
С
позиции теории, такое решение относят к решениям, минимизирующим риск,
и оно требует нахождения оперативной характеристики,
которая определяется следующим образом:
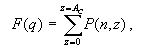
где F(q) - вероятность приемки партии изделий,
среди которых доля дефектных изделий составляет ;
Ac - приемочное число (допустимое число дефектных изделий в выборке
);
P(n, z) - вероятности появления в выборке бракованных изделий,
когда последовательно принимает значения от 0 до Ac.
Иными словами это кумулятивная вероятность и ее можно
определить по формуле:
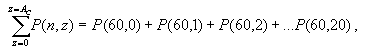
где n для примера взято равным 60, а z заранее
неизвестно и принято в диапазоне 0-20.
Оперативную характеристику можно представить в виде графика
F(q)=f(q%), зафиксировав значение n, при заданных значениях
Ас и N.
Например, используя гипергеометрический закон распределения
при q от нуля до 10, при N= 1200; n = 100 и Ас
= 3 получим:
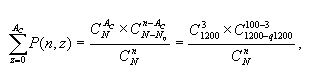
где N =1200 - объем партии;
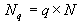 - объем дефектных деталей в партии.
- объем дефектных деталей в партии.
Результаты
расчетов приведены в таб.1. Полученная оперативная характеристика
конроля показана на рис.1.
|
Доля дефектных изделий в партии q(в
%)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Вероятность приемки F(q)
|
1,0
|
0,98
|
0,86
|
0,65
|
0,43
|
0,25
|
0,15
|
0,08
|
0,04
|
0,02
|
0,01
|
Таблица
1. Оперативная характеристика плана приемочного контроля
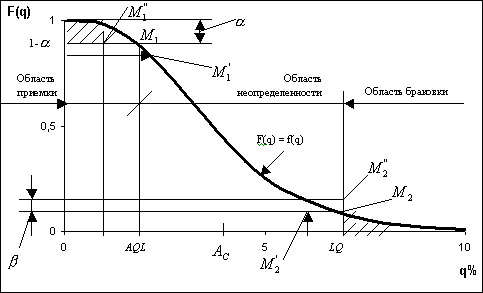
Рис. 1. Оперативная характеристика плана приемочного контроля
На рис.1 показаны: 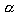 -
риск поставщика; -
риск поставщика; 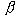 -
риск заказчика; AQL - приемочный уровень дефектности (accept
- принимать; quality - качество; level - уровень); LQ
- браковочный уровень дефектности. -
риск заказчика; AQL - приемочный уровень дефектности (accept
- принимать; quality - качество; level - уровень); LQ
- браковочный уровень дефектности.
На кривой F(q) = f(q) совпадение заданных и 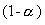 в
точке в
точке 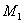 и LQ и
и LQ и 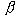 в точке
в точке 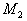 маловероятно,
что и показано на рисунке. Другими словами кривая F(q)=f(q)
должна быть согласована с величинами AQL, маловероятно,
что и показано на рисунке. Другими словами кривая F(q)=f(q)
должна быть согласована с величинами AQL, 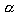 ,
LQ и ,
LQ и 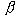 . .
Покажем процедуру использования оперативной характеристики
плана приемочного контроля на численном примере.
Рассмотрим тенденции изменения вида функции F(q)
при изменении величин n, Ac:
1. Допустим, что Ас / n = const, но n и
Ас увеличиваются. Кривая при этом увеличивает свою крутизну и
в пределе, когда n = N, выборочный контроль перейдет в сплошной
и AQL = LQ.
2. Пусть при n = const, Ас увеличивается.
3. Если при n = const, Ас увеличивается,
то контроль становится менее жестким.
4. Ас = const; n увеличивается, контроль
ужесточается.

|

