Существуют много методов оценки качества, однако как только производственный процесс становится управляемым, возникает следующий вопрос: в какой степени долговременное поведение процесса удовлетворяет техническим условиям и целям, поставленным руководством? Рассмотрим, как мы можем оценить пригодность процесса с помощью осмысленных показателей.

Итак, следует различать управляемый и неуправляемый процесс. Заметим, что нет смысла изучать пригодность производственного процесса, если он не управляем. Следовательно, первый шаг к организации высококачественного процесса производства состоит в том, чтобы сделать процесс управляемым (см. )

Если процесс управляем, то можно ставить вопрос о его пригодности. Возвращаясь к примеру с поршневыми кольцами, заметим, что если дана выборка определенного объема, то можно оценить стандартное отклонение процесса, то есть сигма производства поршневых колец. Затем можно построить гистограмму распределения диаметров поршневых колец. Если распределение диаметров нормальное, то можно сделать выводы о доле поршневых колец, попадающих в границы допуска (см. рис.1).

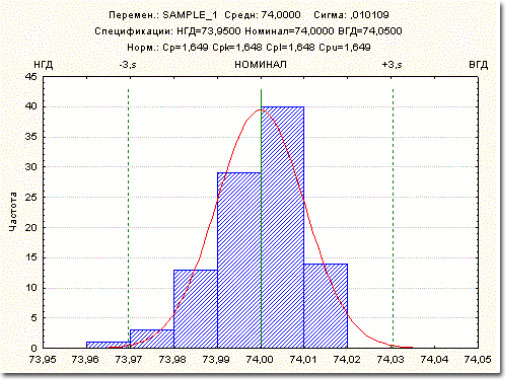
Рисунок 1. Нормальное распределение, границы допуска

Индексы пригодности процесса

Общеупотребительными индексами пригодности процесса являются индексы пригодности (Cp и Cpk), т.к. они достаточно полно отражают отношения технически возможных отклонений (размаха процесса) к ±3 сигма пределам от первоначальных спецификаций.

Для вычислений нам потребуется стандартное отклонение Сигма

1. Находим размах R(i) для каждой выборки, где R(i) = максимальное значение - минимальное значение для i - ой выборки;

2. Вычисляем средний размах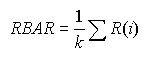

3. Вычисляем сигма 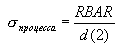, где d(2) можно найти по стандартным статистическим таблицам

n	d(2)
2	1.128
3	1.693
4	2.059
5	2.326
6	2.534
7	2.704
8	2.847
9	2.970

Замечание: стандартное отклонение наблюдений не равно стандартному отклонению средних всех выборок, которое является результатом деления стандартного отклонения на квадратный корень из n (объем выборки).

НГД, ВГД (нижняя и верхняя границы допуска). Обычно технические условия задают некий диапазон допустимых значений. Разность между НГД и ВГД называется размахом допуска.

Формулы индексов пригодности

Потенциальная пригодность (Cp). Это простейший и самый естественный показатель пригодности производственного процесса. Он определяется как отношение размаха допуска к размаху процесса; при использовании границ ±3 сигма данный показатель можно выразить в виде 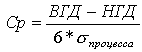. Данное отношение выражает долю размаха кривой (относительно сигма) нормального распределения, попадающую в границы допуска (при условии, что среднее значение распределения является номинальным, то есть процесс центрирован по номиналу).

Нижняя/верхняя потенциальная пригодность (Cpl, Cpu). Недостаток показателя Cp состоит в том, что он может дать неверную информацию о производственном процессе в том случае, если среднее процесса отличается от номинального, иными словами, если процесс не центрирован.
Для пояснения можно провести некоторую аналогию: Вы стреляете по мишени из ружья. Если попадаете точно в яблочко, то это высокий Сp; если же прицел смещен, и Вы все время попадаете в узкую область, лежащую далеко от центра, то Сp будет высоким при низкой потенциальной пригодности процесса.
Нецентрированность (смещенность) процесса производства можно выразить следующим образом. Сначала можно вычислить верхний и нижний показатели пригодности, чтобы отразить отклонение наблюдаемого среднего процесса от НГД и ВГД. Приняв в качестве размаха процесса границы ±3 сигма, вычислим следующие показатели:

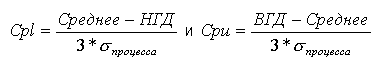
Подтвержденное качество (Cpk). Наконец, Cp можно скорректировать, внеся поправку на нецентрированность посредством вычисления 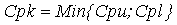. Если процесс идеально центрирован, то Cpk равно Cp, но, при смещении процесса смещается от своего номинального значения, Cpk становится меньше Cp.
Высокий Cpk будет только в том случае, когда цель достигнута при минимальном отклонении от среднего.
Для понимания смысла индекса производительности рассмотрим еще один простой пример: у Вас есть гараж и машина, которую надо поставить внутрь гаража. Гараж определяет допустимые пределы, машина - результат процесса. Если машина только чуть-чуть меньше, чем гараж, то Вам лучше поставить ее ближе к правой стороне гаража, если Вы хотите потом из нее выйти. Если машина шире, чем гараж, то Вы можете попробовать поставить ее посередине за гаражом, тогда гараж не имеет смысла. Если машина намного меньше, чем гараж (процесс Шесть Сигма), Вы можете поставить ее точно посередине гаража, ближе к правой стороне или даже к левой - по вашему желанию. Если процесс с маленькой дисперсией, то Вы сможете поставить машину внутри гаража и этим удовлетворить требования клиентов. Cpk определяет отношение между размерами машины, размерами гаража и тем, насколько далеко от середины Вам надо ставить машину. Пусть результат процесса (машина) может расширяться перед попаданием в границы спецификаций (дверь гаража):
· Cpk=1/2 – Вы врезались в край двери;
· Cpk=1 – Вы слегка поцарапали машину о край двери;
· Cpk=2 – все в норме, даже если Ваша ширина возрастет чуть меньше, чем в 2 раза;
· Cpk=3 – а теперь можете расширяться почти в 3 раза.

Индексы производительности процесса

При контроле процесса с помощью карт контроля качества (например, X- или R-карты, см. ) часто бывает полезно вычислять показатели пригодности процесса. Когда набор данных состоит из нескольких выборок, то можно вычислить два разных показателя изменчивости. Один из них – обычное стандартное отклонение для всех наблюдений, не принимающее в расчет, что данные состоят из нескольких выборок; другой показатель оценивает собственный разброс процесса по изменчивости внутри выборки. Если при стандартных вычислениях пригодности используется общая изменчивость процесса, то полученные показатели обычно называют показателями качества процессам Pp и Ppk (process performance) (поскольку они описывают фактическое поведение процесса).
Индекс производительности процесса по существу пытается подтвердить то, что полученная Вами выборка способна удовлетворить требования клиентов. Производительность процесса используется только, когда контроль не может быть осуществлен (Например, при пробном производстве небольшого числа изделий).
Индекс Cpk краткосрочный, а Ppk – долгосрочный. Cpk говорит, что Ваш процесс сможет делать в будущем. Ppk говорит, насколько хорошо процесс был представлен в прошлом. Вы не можете использовать этот показатель в будущем, как Cpk, потому что процесс не подвергается непрерывному контролю. Значения Cpk и Ppk стремятся почти к одному и тому же значению, когда процесс статистически контролируется. Это происходит из-за того, что в этом случае сигма =стандартное отклонение. Если контроль не осуществляется, значения, естественно, будут различными, разница, возможно, будет достаточно велика.
Реалистичней использовать Pp и Ppk, чем Cp или Cpk, так как дисперсия процесса не сочетается с разбиением на выборки. Однако, Cp и Cpk могут быть очень полезны при определении попадания пригодности процесса в определенные границы. Это даст Вам наилучший сценарий развития существующего процесса.

Формулы индексов производительности

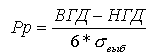
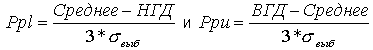
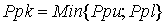
где 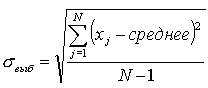– стандартное отклонение выборки

Негауссовские распределения

Рассмотрим что делать, если распределение соответствующего параметра качества или переменной (например, диаметров поршневых колец) не является нормальным.
Если того требует поставленная задача, гистограмму можно аппроксимировать отличным от нормального распределением и вычислить показатели пригодности с помощью метода процентилей. Для всех распределений можно также вычислить таблицы ожидаемых частот, ожидаемое число наблюдений, выходящих за рамки технических условий, и построить графики квантиль-квантиль и вероятность-вероятность.

Негауссовские индексы пригодности
Как уже отмечалось ранее, показатели пригодности в общем случае вычисляются для того, чтобы оценить качество процесса, т.е. чтобы получить оценки разброса производимых изделий (размах процесса) по отношению к размаху допуска. Для стандартных показателей пригодности процесса, основанных на нормальном распределении, размах процесса обычно определяется как 6 сигма, т.е. как плюс-минус утроенная оценка стандартного отклонения процесса. Для стандартной кривой нормального распределения эти границы (zl = -3 и zu = +3) пересчитываются в 0.135 и 99.865 процентили соответственно. Для распределений, отличных от нормального, границы 3 сигма, а также среднее (zм = 0.0) можно заменить соответствующими стандартными значениями, дающими те же величины процентилей под кривой негауссовского распределения.

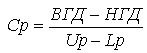
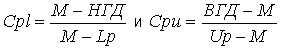
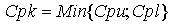
где M – медиана (50 процентиль) соответствующего распределения,
Up и Lp – 99.865 и 0.135 процентили соответственно.
Обратите внимание, что значения Up и Lp могут быть другими, если размах процесса задан другими границами (например, ±2 сигма).