В экономической литературе встречаются различные определения логистики. Приведем некоторые из них.

Логистика (Logistics) это:

1. Планирование и обеспечение материально-технического снабжения, подготовки и передвижения людского состава.
2. Организация службы тыла.
3. Материально-техническое снабжение магазина.
4. Тыл и снабжение, материально-техническое снабжение, работа тыла.
5. Движение материалов и запасов.
6. Наука о планировании, организации, управлении, контроле и регулировании движения материальных и информационных потоков в пространстве и во времени от их первичного использования до конечного потребителя.

Логистику также определяют как научное направление, связанное с поиском новых возможностей повышения эффективности материальных потоков.

Понятие логистики сначала появилось в военной сфере, где охватывало проблемы транспорта, снабжения, перемещения войсковых подразделений. Затем понятия и методы логистики были перемещены в гражданскую сферу, где использовались в управлении материальными потоками в сфере обращения и производства. При этом понятия логистики и методы логистики стали применяться в экономике сравнительно недавно.

В логистике испотльзуются экономические, экономико-математические и статистические методы для решения различных теоретических и практических задач. Важной задачей логистики является создание интегрированной системы регулирования и контроля материальных и информационных потоков.

В качестве формы существования материального потока обычно рассматриваются запасы. Логистика решает задачи вычисления объемов запасов, обеспечивающих наиболее экономным путем удовлетворение будущего (и зачастую неопределенного на момент расчетов) потребительского спроса на товары и услуги компании. Минимизируются суммарные затраты, связанные с заготовками, хранением продукта и убытками из-за неудовлетворенного спроса. В тоже время чрезмерно большой запас связан с омертвением капитала, требует значительных расходов на хранение и уход за продуктом.

Рассмотрим типичную задачу оптимизации оборота товара на складе. Имеется предприятие, производящее телевизоры. Сделки происходят по следующей схеме: в офис от клиента поступает заказ (например, количество телевизоров, которое необходимо покупателю). Далее, заказ оформляется и подается заявка на предприятие о доставке на склад партии товара для дальнейшей его отгрузки покупателю. Затраты, связанные с выполнением одной доставки партии с предприятия на склад, равны Ctr (transporting cost). Месячные затраты на хранение на складе одного телевизора равны Cst (storage cost). Ожидаемая потребность в товаре у покупателей составляет D (demand) единиц в месяц. Необходимо оценить оптимальное количество телевизоров R*, которое следует указывать в заявке на предприятие.

В задаче минимизируется функция издержек. Изжержки состоят из двух компонент: хранения готовой продукции на складе и доставки продукции на склад. Считаем, что отгрузка готовой продукции происходит равномерно. Тогда график убытия запасов со склада выглядит следующим образом:

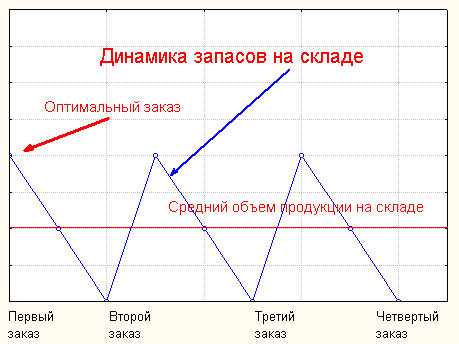
Рис. 1. Динамика запасов на складе

Издержки доставки партии продукции на склад равны Tr = Ctr ·  N, где N - число заказов за месяц. N = D / R*.

Издержки хранения готовой продукции на складе равны Tst = H ·  Rm, где Rm -средний объем продукции на складе. Rm = R*/2 (см. Рис. 1). Тогда функция издержек представляет собой сумму

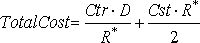
Минимизируем данную функцию по R*. Для этого дифференцируем ее по R* и приравниваем производную к нулю. Из получившегося уравнения получаем значение оптимального заказа:

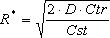(1)

Ключевым моментом в решении данной задачи является оценка ожидаемой потребности в продукте в ближайший месяц. По своей природе это задача прогнозирования. На основе внешних факторов, влияющих на спрос, нужно предсказать с достаточной степенью точности параметры заказов: число, объемы или совокупная стоимость (если продуктом являются финансовые ресурсы).

 
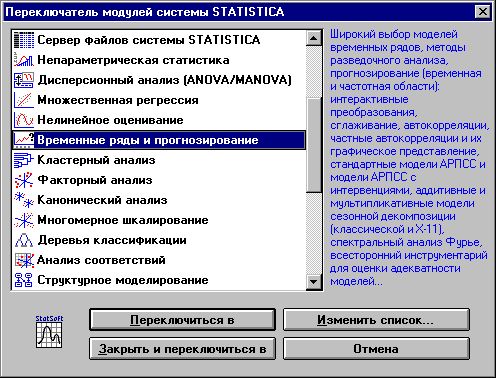
Рис. 2. Окно переключателей модулей STATISTICA

На предприятии собирается статистика по месячным продажам телевизоров в течение 11 лет. Файл данных в системе STATSITICA выглядит следующим образом:

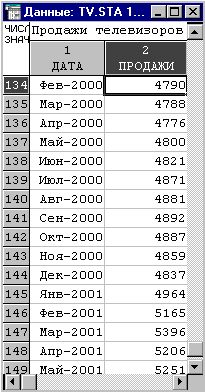
Рис. 3. Файл данных по продажам телевизоров

Первым шагом при решении задачи прогнозирования является визуализация временного ряда. График продаж выглядит следующим образом:

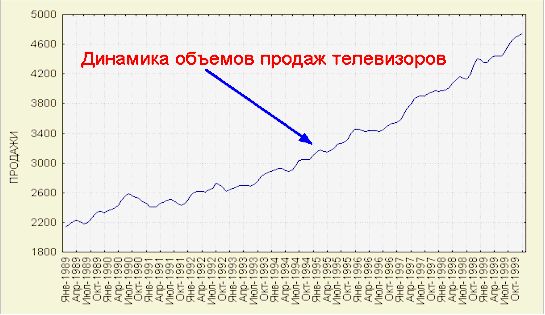
Рис. 4. Динамика объемов продаж телевизоров

Наиболее распространенным способом прогнозирования является описание временного ряда некоторой математической моделью, на основе которой предсказываются будущие значения. Чаще всего используются линейные модели, которые довольно хорошо аппроксимируют экономические показатели.

Первым шагом будет проверка ряда на стационарность, поскольку практически вся теория прогнозирования линейных моделей хорошо работает именно на стационарных рядах. Ищем автокорреляционную функцию для показателя. Для стационарных рядов автокорреляционные коэффициенты должны стремиться к нулю с течением времени.

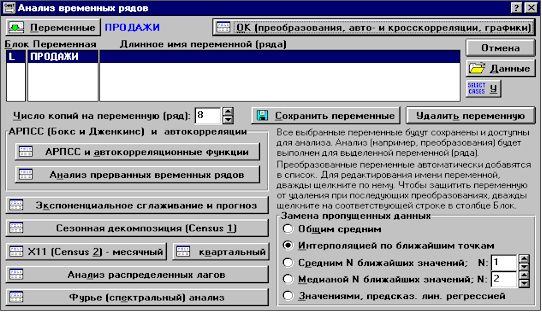
Рис. 5. Окно методов модуля "Временные ряды и прогнозирование"

Автокорреляционная функция ряда:

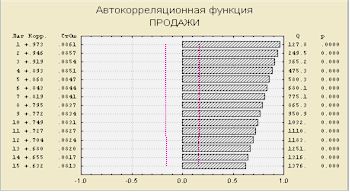
Рис. 6. Автокорреляционная функция

Значения автокорреляционной функции ряда не стремятся к нулю с течением времени, следовательно, ряд нестационарный. К стационарному виду его можно привести, взяв его первую разность.

Графики первой разности и ее автокорреляционной функции:

Рис. 7. Динамика первой разности ряда ПРОДАЖИ и ее автокорреляционной функции

Вид автокорреляциооной функции позволяет говорить о стационарности первой разности ряда продаж и о налияии линейного тренда в первоначальном ряде.

Исследуем ряд на периодичность. Воспользуемся методами спектрального анализа Фурье. Цель анализа - разложить временной ряд с циклическими компонентами на несколько основных синусоидальных функций с определенной длиной волн. В результате можно обнаружить несколько повторяющихся циклов различной длины, которые на первый взгляд выглядят, как случайный шум. Результаты анализа представляются на периодограмме, где показаны вклады различных периодов в динамику ряда.

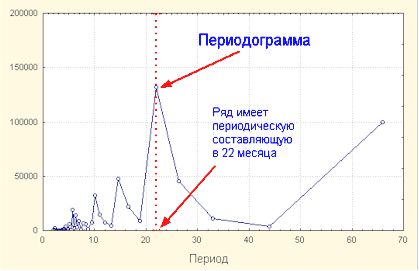
Рис. 8.  Результаты спектрального анализа - периодограмма

На периодограмме четко выделяется периодическая составляющая в 22 месяца. Экономическая интерпретация данного факта может быть следующая - 22 месяца - срок, тесно связанный с периодичностью появления на рынке новых моделей телевизоров. Потребительский спрос в это время возрастает, после чего наступает период некоторого спада покупательской активности.

Переходим к прогнозированию.  Одним из эффективных методов построения прогноза является экспоненциальное сглаживание. Идея этого метода достаточно прозрачна - временной ряд прогнозируется на основе своих предыдущих значений, причем им придаются веса, экспоненциально убывающие по мере удаления от текущего момента времени.

Рис. 9. Окно выбора параметров модели экспоненциального сглаживания

Используем информацию, полученную на предыдущих шагах - выбираем модель Холта с линейным трендом, устанавливаем период сезонной компоненты, равный двадцати двум месяцам. Остальные параметры экспоненциального сглаживания оцениваем методом автоматического поиска на сетке. Одновременно строим прогноз на 10 месяцев вперед. Результаты оценивания:

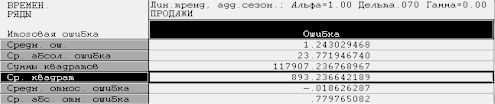
Рис. 10. Окно результатов сглаживания

Динамика ряда продаж и прогоноза показана на рисунке 11.

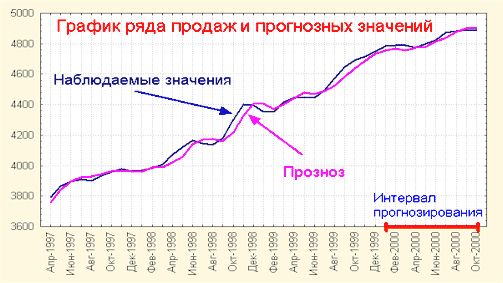
Рис. 11. Динамика ряда продаж телевизоров и прогнозных значений

Другой достаточно популярный метод прогнозирования - прогнозирование ARIMA моделью. Окно выбора параметров модели показано на рисунке 12.

Рис. 12. Выбор параметров модели

Параметры ARIMA - модели указываем, используя информация, полученную на предыдущих шагах: нужно анализировать первую разность ряда, поскольку исходный ряд нестационарен, сезонная компонента равна двадцати двум месяцам. Кроме этого, в модель входят еще два авторегрессионных члена (p=2 в окне выбора параметров). Результаты оценивания:

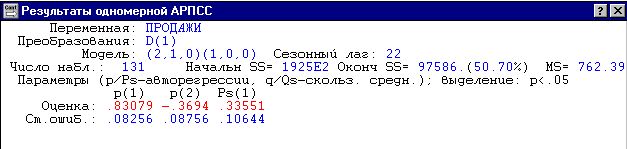
Рис. 13. Результаты оценивания ARIMA модели

График ряда и прогноза:

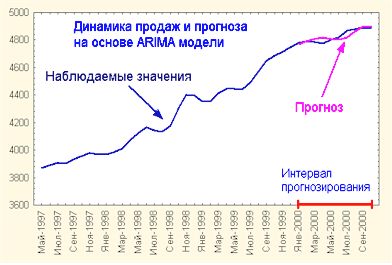
Рис. 14. Динамика продаж и прогноз ARIMA моделью

Приведем сравнительный график прогнозов экспоненциальным сглаживанием и ARIMA - моделью:

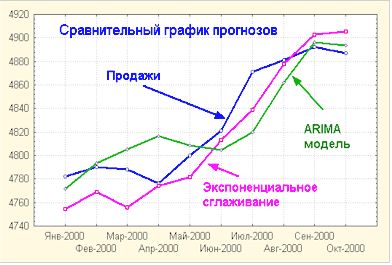
Рис. 15. Сравнение качества прогнозов

ARIMA  - модель дает более точный краткосрочный прогноз, в то же время экспоненциальное сглаживание лучше отражает долгосрочноу поведение ряда.

Возвращаемся к первоначальной задаче логистики - нахождении оптимального размера заказа. После того, как построен прогноз продаж телевизоров на несколько месяцев, делается предположение о том, что спрос D и предложение в эти месяцы будут совпадать, следовательно, оценку продаж можно использовать в качестве оценки ожидаемого спроса D на телевизоры.

Теперь по формуле (1) можно определить оптимальный заказ R*:

 .
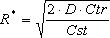