В этом примере воспроизводится экспериментальный план, реализованный инженером фабрики по изготовлению пластиков (пример адаптирован из кн.: Cornell J.A. (1990). How to Apply Response Surface Methodology, vol. 8 in Basic References in Quality Control: Statistical Techniques, edited by S.S. Shapiro and E. Mykytka. Milwaukee: American Society for Quality Control).

Задача состояла в том, чтобы исследовать факторы, влияющие на износ пластиковых дисков.

Два фактора оказывают наибольшее влияние на износ:
1) материал, характеризующийся отношением наполнителя к эпоксидной резине,
2) расположение диска в форме.

В качестве зависимой переменной рассматривалась плотность полученного диска.

Сначала использовалась дробный факторный план 22 для того, чтобы определить адекватность модели первого порядка.

Но оказалось, что эта модель оказалась адекватной лишь для некоторой области значений факторов и неадекватной для всей значений.

Поэтому было решено использовать центральный композиционный план и применить модель второго порядка.

Построение плана
Центральный композиционный план может состоять из куба и звезды. Куб соответствует полному факторному плану - точки эксперимента располагаются в вершинах куба (фактически это факторный план 22).

Звезда содержит дополнительное множество точек, расположенных на одинаковых расстояниях от центра куба на отрезках, исходящих из центра и проходящих через каждую сторону куба.

В данном исследовании применялся ротатабельный план, для которого дисперсия отклика является постоянной во всех точках, одинаково удаленных от центра плана.

Пусть фактор A - это материал, из которого изготовлен диск, более точно, переменная disk composition ratio (композиционное отношение), фактор B - положение диска в форме (position of disk in mold).

Зависимая переменная или отклик – это плотность диска (Thickness).

Запустим модуль Планирование эксперимента.

На стартовой панели выберем Центральные композиционные планы, поверхности отклика и нажмем кнопку OK.

В появившемся диалоговом окне выберем опцию Построение плана, а в поле Факторы/блоки/опыты - строку 2/1/10. Нажмем кнопку OK.

Появится диалоговое окно План эксперимента для поверхности отклика. Нажмем на кнопку Имена факторов, значения и заполним таблицу в диалоговом окне Итоги для переменных так, как показано на рис. 1.

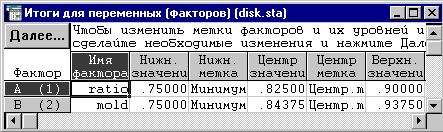
Рис.1. Диалоговое окно для описания факторов

Нажмем кнопку Далее и выберем опции для настройки отображения плана так, как показано на следующем рисунке. Сделайте точно все показанные настройки, чтобы получить нужный результат!

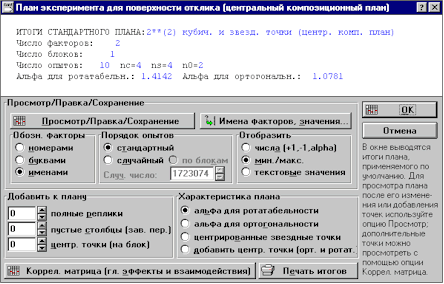
Рис.2. Диалоговое окно для задания параметров композиционного плана

Просмотрим план. Для этого нажмем Просмотр/Правка/Сохранение.

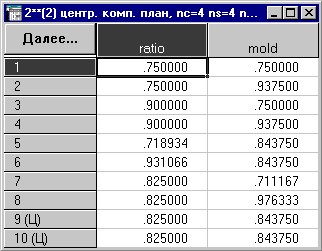
Рис.3. Итоги плана

Задание имени и сохранение экспериментального плана

Выберем Файл|Сохранить как файл данных…; появится соответствующее диалоговое окно (рис. 4).

Зададим имя плана disk.sta и нажмем кнопку OK (рекомендуем вам открыть готовый файл disk.sta).

Рис.4. Сохранение плана

Вернемся вновь в диалоговое окно План эксперимента для поверхности отклика.

Нажмем кнопку Печать итогов. В зависимости от настроек вывода в диалоговом окне Параметры страницы/вывода результаты плана будут распечатаны на принтере или выведены в отчет.

В построенной таблице показан порядок сбора экспериментальных данных.

Далее эксперимент был приведен и данные занесены в табл. 1.

Анализ экспериментальных данных

Проведем анализ полученных данных.

В диалоговом окне План эксперимента для поверхности отклика нажмем кнопку Отмена.

Мы возвратимся к диалогу Центральные композиционные планы.

Рис.5. Выбор опций построения/анализа плана

Выберем опцию Анализ результатов. Нажмем кнопку Переменные. Зададим thick в качестве зависимой переменной, ratio и mold в качестве независимых переменных и block в качестве блоковой переменной.

В поле Для перекодирования использовать оставим принятое по умолчанию положение уровни факторов из файла данных. Теперь нажмем OK.

На экране появится следующее окно STATISTICA.

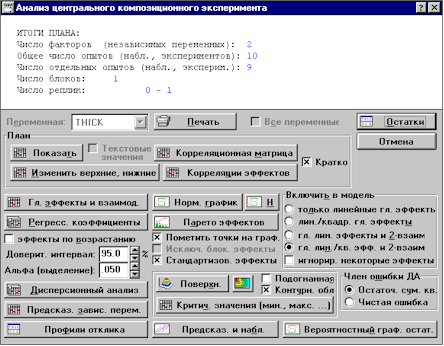
Рис.6. Получение результатов анализа плана

Прежде всего оценим адекватность модели второго порядка.

Для оценки адекватности воспользуемся таблицей дисперсионного анализа и графиками.

На панели Включить в модель выберем опцию гл. лин./кв. эфф. и 2-взаимодействия, а на панели Член ошибки ДА – Остаточная сумма квадратов.

Нажмем на кнопку Дисперсионный анализ.

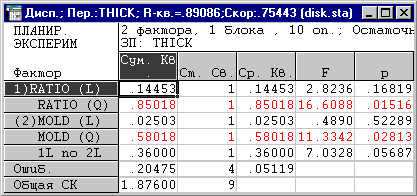
Рис.7. Таблица дисперсионного анализа

Из этой таблицы следует, что статистически значимые эффекты (уровень p<0.05) имеют два квадратичных члена ratio (Q) и mold (Q).

Для того чтобы определить, насколько модель хорошо описывает экспериментальные данные, будем использовать тест lack-of-fit (потери согласия).

Вернемся к диалоговому окну результатов анализа, выберем Чистую ошибку для Члена ошибки ДА и снова нажмем кнопку Дисперсионный анализ. Система добавит в таблицу значения потери согласия и чистой ошибки.

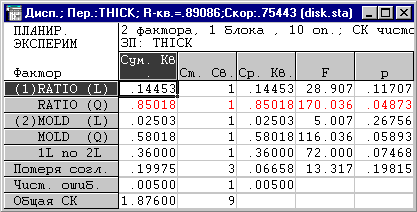
Рис.8. Таблица дисперсионного анализа с дополнительным тестом

Вследствие того, что p-значение использованного дополнительного теста больше 0.05, модель второго порядка представляется адекватной для описания отклика.

Установим Член ошибки ДА снова в положение Остаточная сумма квадратов.

Теперь рассмотрим вероятностный график.

Для этого нажмем на кнопку Нормальный график.

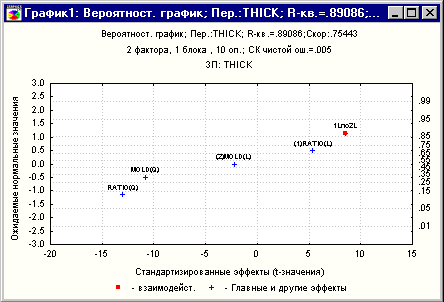
Рис.9. График эффектов нормального распределения вероятностей

Из рисунка видно, что квадратичные члены с меткой Q находятся в стороне от линии нормального распределения, что указывает на статистическую значимость их влияния на отклик.

Рассмотрим также карту Парето. Нажмем на кнопку Парето эффектов.

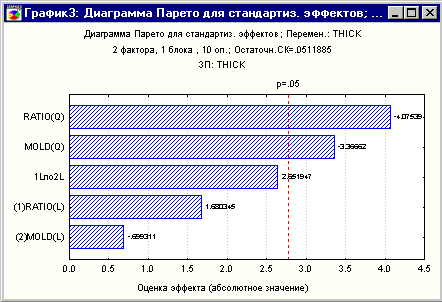
Рис.10. Карта Парето

Итак, квадратичные члены модели дают значимые эффекты. Соответствующие им колонки пересекают вертикальную линию, которая представляет 95% доверительную вероятность.

Определим теперь область значений факторов, в которой плотность пластиковых дисков является максимальной.

Для этого лучше всего использовать график поверхности отклика. Нажмем на кнопку Поверхность.

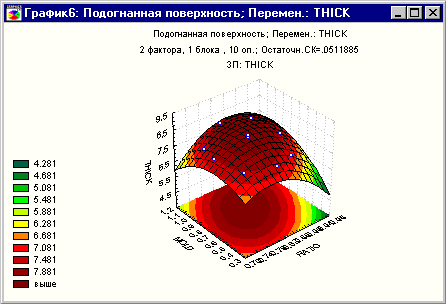
Рис.11. График поверхности отклика

Эта поверхность имеет экстремум, равный примерно 0.9.

Для более детального рассмотрения области максимума целесообразно рассмотреть контурный график (цветная квадратная кнопка рядом с кнопкой Поверхность). На графике показаны линии уровня поверхности. Это весьма удобно для исследования поверхности.

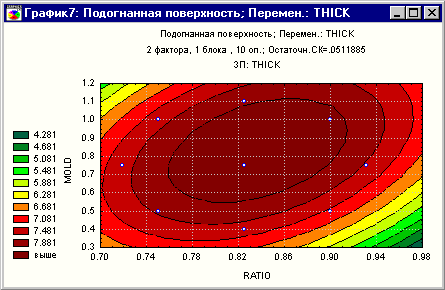
Рис.12. Контурный график

Посмотрите на цветовые метки, расположенные слева от графика. Эти метки, показывающие интенсивность цветов, позволят вам легко соориентироваться и понять, что максимальная плотность достигается при изменении параметров в центральном эллипсе, положение главных осей которого легко оценить графически.

Например, максимально прочные диски будут получены при значениях disk composition ratio, изменяющихся от 0.78 до 0.86, и значениях mold, изменяющихся от 0.6 до 0.9.

Более строго: все значения независимых переменных, попадающие в центральный эллипс, приводят к наивысшему качеству пластиковых дисков.

Более подробная информация содержится в специальных материалах StatSoft.