Описание объекта и цель исследования

Анализировалась структура поставщиков предприятия. Поставляемая продукция представляет собой сырье для производства конечного продукта на предприятии. Качество сырья поставщиков различается. Каждый поставщик характеризуется месячным объемом поставок. Рассматривалось 11 поставщиков.

Конечный продукт характеризуется выходным параметром, который является показателем его качества. На выходной параметр оказывает влияние структура поставщиков (поскольку сырье различается по качеству, то в зависимости от объема поставок того или иного поставщика параметр качества будет меняться). Характер зависимости выходного параметра от объема поставок каждого поставщика неизвестен.

Целью исследования является анализ влияния объемов поставок каждого поставщика на значения выходного параметра, характеризующего качество продукции.

Стояла задачи построение математической модели, описывающей характер влияния объемов поставок каждого поставщика на выходной параметр.

В ходе решения задачи рассматривалась также классификация поставщиков по степени их влияния на исходный показатель.

Исходные данные представляют месячные ряды объемов поставок каждого поставщика и значения выходного показателя.

Мы проводим анализ последовательно в соответствии с технологиями

На предварительном этапе производится организация данных для последующего анализа в системе STATISTICA. Данные представлены следующим образом: столбцы соответствуют поставщикам, строки – масяцам. Таким образом, каждый столбец представляет собой временной ряд месячных объемов продаж каждого поставщика.

Если поставщик не поставлял продукцию в текущем месяце, то в соответствующих ячейках стоят нули.

Файл данных приведен на рисунке.

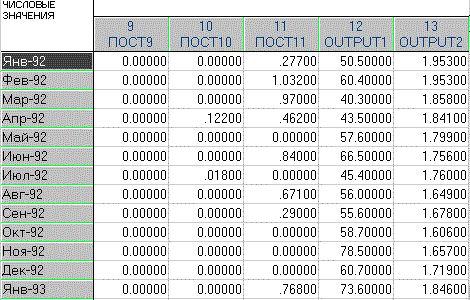
Рис.1. Файл данных к задаче в формате STATISTICA

Разведочный анализ

Представим графически зависимость выходного параметра от объемов поставок каждого поставщика:

Анализ диаграмм рассеяния позволяет говорить о том, что статистически значимое влияние на выходную переменную могут оказывать поставщики 2, 3, 5, 8, 9, 11. Влияние поставщиков 4, 7 статистически незначимо – выходной параметр слабо зависит от изменения в их объемах продаж.

Динамика объемов продаж на исследуемом промежутке времени:

                                 

                                 

                                 

                                 
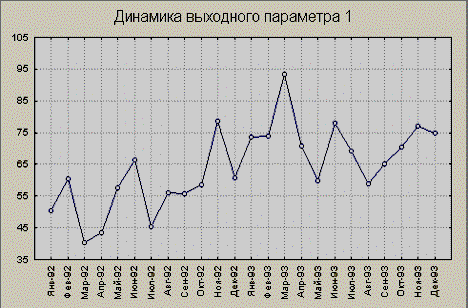Рис.3. Динамика объемов поставок каждого поставщика и динамика выходного параметра

Классификация поставщиков

Проведем классификацию поставщиков по степени их влияния на выходной показатель. Для этого воспользуемся методами модуля “Кластерный анализ” системы STATISTICA. Проведем классификационный анализ поставщиков. Его целью является определение степени сходства поставщиков друг с другом. Процедура носит название “Древовидная кластеризация”. Результаты следующие:

Рис. 4. Результаты древовидной кластеризации множества поставщиков

Диаграмма классификации иллюстрирует разбиение поставщиков на группы. Анализируя ее, можно, например, утверждать, что поставщики 4, 5, 6, 7, 9, 10 оказывают сходное влияние на выход продукции. Следовательно, можно говорить о сходстве качества сырья у данных поставщиков.

Построение модели. Строим регрессионную линейную модель влияния объемов поставок на выходную переменную, т.е. будем приближать выходную переменную формулой:

Output = A₁ + A₂*Пост₁ +…A₁₁*Пост₁₁ + e

– линейная зависимость от объемов продаж каждого поставщика с неизвестными коэффициентами. e – случайная компонента с нулевым математическим ожиданием.

Задача состоит в том, чтобы оценить неизвестные коэффициенты. Для построения регрессионной модели и численной оценки коэффициентов перед объемами продаж поставщиков воспользуемся модулем STATISTICA “Множественная регрессия”.

Все оценки строятся легко в диалоговом режиме. Программа автоматически найдет лучшую модель, т.е. исключит поставщиков, влияние которых на выходной параметр очень слабое, и оставит в модели поставщиков, которые действительно оказывают значимое влияние на исследуемую переменную.

Рис. 5. Указание зависимой переменной и независимых факторов

Рис. 6. Окно результатов расчетов коэффициентов регрессии. Красным цветом выделены статистически значимые независимые переменные, синим – незначимые переменные

Окончательная формула для расчета выходного показателя в линейной спецификации следующая:

Output = 162.3 - 46.8*Пост₁ – 36.8*Пост₂ –19.9*Пост₃ – 58.8*Пост₅ –

38.4*Пост₆ – 38.1*Пост₈ – 150.1*Пост₁₀ – 38.2*Пост₁₁

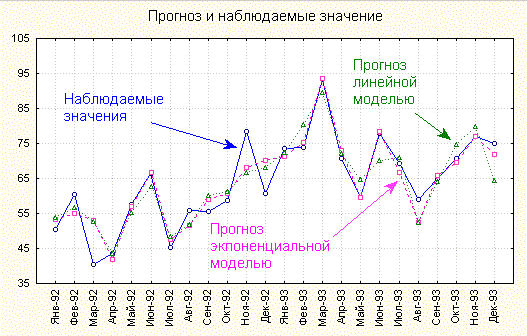
Результаты численного оценивания модели позволяют построить прогноз параметра 1:

Рис. 7. Наблюдаемые значения и прогноз

Определим оптимальное множество поставщиков. Для этого проведем анализ модели на избыточность. Наша цель - проверить обоснованность вхождения всех поставщиков в модель. Проверка проводится методом расчета показателя толерантности для каждой независимой переменной в уравнении. Толерантность переменной показывает, насколько велика ее связь с остальными независимыми переменными. Если связь достаточно велика, то использование данной переменной нецелесообразно и является избыточным. Следовательно, ее можно исключить из модели без большой потери в объясняющих свойствах. В итоге мы получим некоторое множество поставщиков, влияние которых на исследуемый параметр 1 наиболе значимо, причем будет устранена избыточность переменных. С экономической точки зрения избыточность вхождения поставщика в модель означает его слабое влияние на выходной параметр. Целесообразно проводить закупки только у тех поставщиков, качество сырья которых достаточно сильно влияет на параметр 1. Это даст экономию финансовых ресурсов без большого ущерба для параметра 1 конечной продукции предприятия. Результаты проверки на избыточность:

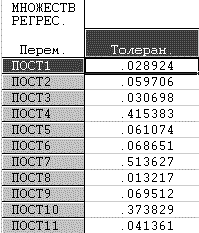
Рис.8. Толерантность для многих переменных низкая, что говорит о том, что спецификация модели нуждается в улучшении

Реализуем следующий алгоритм поиска оптимальной спецификации модели. Будем включать или исключать из модели независимые переменные на каждом шаге регресии (на первом шаге используем одну переменную, на втором добавляем еще одну и смотрим на результаты. Если значимость коэффициентов ухудшилась, то ищем другую комбинацию из двух переменных). В результате получим оптимальную спецификацию модели. Алгоритм реализован в модуле "Множественная регрессия". Вызвать его можно, выбрав опцию "Пошаговая регрессия с включением":

Рис.9. Выбор опции "Пошаговая регрессия с включением"

Результаты работы алгоритма:

Рис.10. Результаты работы алгоритма пошаговой регрессии с исключением

Алгоритм поиска оптимальной спецификации оставил в модели две переменных: поставщика 3 и поставщика 9. Это оптимальные поставщики для предприятия с точки зрения их влияния на параметр 1. Численное оценивание коэффициентов дает следующие результаты:

Рис.11. Итоги численного оценивания модели с оптимальными поставщиками

Характер влияния всех поставщиков на выходной показатель отрицательный. Значение скорректированного R² = 0.708  довольно высокое для такого количества наблюдений и данной структуры входных переменных, что говорит о достаточно хороших объясняющих свойствах модели.

Первый столбец на рисунке содержит численные значения оценок коэффициентов модели при объемах поставок для каждого поставщика. Интерпретация коэффициентов следующая: при изменении объема поставок для некоторого поставщика на единицу (единицей считается единица измерения представленных данных) значение выходного показателя меняется на величину соответствующего коэффициента в данном столбце.

Построим теперь нелинейную модель влияния поставщиков на выходной параметр 1, которая называется модель экспоненциального роста:

Output = C + exp(b₀ + b₁*Пост₁ + … + b₁₁*Пост₁₁)

Оценивание коэффициентов проводится с использованием методов модуля STATISTICA “Нелинейное оценивание”. Применяем метод оценивания коэффициентов Хука-Дживиса.

Результаты оценивания:

Окончательная формула для расчета выходного показателя в рассматриваемой спецификации следующая: