Виктор Э. Кейн

(Компания Форд Мотор, отдел трансмиссии и шасси, П. О. бокс 2097(7) Ливония, М1 48150)

Индексы воспроизводимости C_p,CPU, CPL, k и C_pk представляют параметры процесса и тесно связаны с ними. Известно, что эти индексы образуют полную систему показателей работы процесса и могут использоваться и с двусторонними, и с односторонними допусками, и с заданными номиналами, и без них. Многие японские предприятия в разных отраслях промышленности постоянно применяют эти 5 индексов, и автомобильная промышленность США тоже начала их применение во многих областях. В статье рассматриваются различные применения этих индексов, а также их связь со статистическими свойствами выборок.

Введение

Количественное представление (квантификация) настройки процесса и его вариации - основа для понимания качества изделий в любом производстве. Представим себе ситуацию, когда среднее арифметическое процесса m и стандартное отклонение s , неизвестны и оцениваются через ` х и s, соответственно. С практической точки зрения ` х и s не безразмерные, а иногда и неудобные статистические свертки, если учесть сотни показателей на предприятии или у поставщиков. Во многих ситуациях индексы воспроизводимости можно использовать для выяснения соотношений между параметрами процесса m и s и инженерными требованиями, которые могут включать в себя односторонние и двусторонние допуски с заданными значениями (номиналами) или без них. Полученные в результате индексы безразмерны и создают общий легко понятный язык для количественной характеристики процесса.

Автомобильная промышленность в настоящее время прилагает много усилий для внедрения статистического управления процессами (СУП) на своих предприятиях и у поставщиков. Индексы воспроизводимости, получаемые из СУП, нашли широкое применение не только для оценки процесса, но и для принятия решений о закупках. В частности представляют интерес индексы C_p и C_pk, применяемые в Японии (Сулливан (1984, 1985 ), а с недавнего времени в автомобильной промышленности США (например, компанией Форд Мотор (1984). Эти индексы показывают соотношение между естественным допуском (6s ), который принят в американской литературе по контролю качества (см., Джуран и Грыня (1980, р. 299) и инженерными допусками. Цель данной статьи - исследовать возможные применены индексов воспроизводимости в связи с их выборочными свойствами и методами оценивания. При обсуждении постулируется, что выход процесса распределен приближенно нормально, а сам процесс находится в статистически управляемом состоянии, Далее “крышечка” ^ будет обозначать оцениваемую величину.

Потенциал процесса

Индекс C_p. Производственные процессы проходят определенные этапы разработки прежде, чем начнется само производство. Эти этапы “подтверждают” проверки на станках поставщика, пусконаладочные испытания станков и производственного оборудования и предпусковые испытания всех режимов для выяснения того, способно ли оборудование производить в ходе производства изделия, удовлетворяющие требованиям . технических условий. Типичный подход - выяснение того, попадает ли естественный допуск процесса (6s ) внутрь границ допуска. Альтернативная формулировка, применяемая в Японии (Сулливан, 1984) - оценить индекс воспроизводимости C_p Эти величины - просто разные способы соотношения допустимого разброса процесса (допуск на изделие) и фактического разброса процесса (естественный допуск), как показано на рис. 1, где ВГД- верхняя граница допуска, НГД -нижняя граница допуска, a NT - естественный допуск. Показатель потенциала процесса равен:

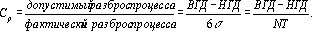(1)

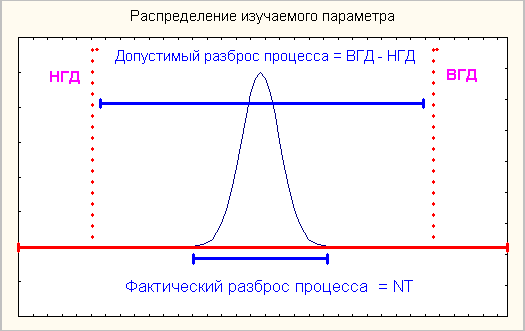
Рис. 1. Соотношение параметров С_р.

Величина C_p=1,0 указывает, что процесс признается “воспроизводимым”, как показано на рис. 2. Вообще надо оценивать стандартное отклонение процесса в формуле (1) для получения оценки воспроизводимости процесса C_p^. Из-за выборочной вариации и ограничений измерительного оборудования, обсуждаемых ниже, C_p^=1,0 обычно не используется как минимальное приемлемое значение.

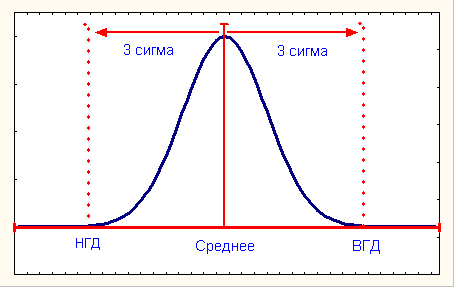
Рис.2. Распределение отдельных деталей для воспроизводимого процесса (Ср=1)

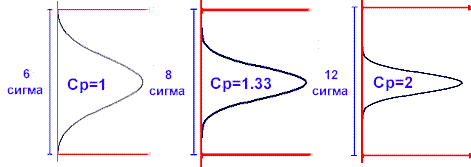
Рис.3.  Индексы Ср для различных диапазонов распределения процесса

Процент допуска	100	75	50
Брак	0.27%	84 части на миллион	>0.1 части на миллион

Таблица 1

Воспроизводимый процесс, в основе которого лежит стабильное нормальное распределение, теоретически дает в результате 0,27% изделий с параметрами, выходящими за пределы допусков. Значение 1,0 было выбрано для демонстрации связи C_p со стандартным шестисигмовым отклонением, используемым в контрольных картах. Если процесс точно воспроизводим, то:

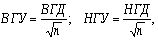(2)

где ВГУ - верхняя граница управления;

НГУ-нижняя граница управления;

n - объем выборки для подгруппы на контрольной карте.

Соотношение в формуле (2) указывает, что границы допуска, скорректированные на объем выборки, равны контрольным границам для процесса с C_p=1,0.

Первоначально C_p использовалось для проведения сравнений разного рода. На рис. 3 показано, как различные значения C_p относятся к разбросу процесса с учетом ширины допуска. Минимальное значение C_p=1,33 обычно применяется к текущему процессу (см. Джуран, Грыня и Бингхем (1979 р. 9-22 ). Оно отражает очень низкую долю брака (0,007%) и таким образом служит ориентиром для эффективной стратегии предотвращения, производства бракованных изделий. Значение C_p=1,33 часто используется для оценки качества оборудования, так как долговременный статистический контроль обычно нельзя организовать во время сертификационных испытаний. Применение показателя 1,33 дает некоторую гарантию, что по крайней мере сохранится C_p=1,0, если в процессе производства возникнут, как подсказывает опыт, дополнительные источники вариации. Следует заметить, что по-видимому более естественно применять традиционный показатель:

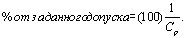
Мотивация к применению C_p вместо % от допуска (или “отношение воспроизводимости” из работы Шарбонно и Вебстера, 1978) связана с естественным соотношением между потенциалом процесса, количественно выраженным C_p, и работоспособностью процесса, количественно выраженной показателем C_pk, который описывается в следующих разделах. Существуют еще естественные обобщения показателя C_p на односторонние допуски и многомерные номиналы.

При изучении потенциала станка часто не учитывается, управляем ли станок в статистическом смысле. Это явно нецелесообразно, так как многие простые проблемы нельзя обнаружить, если не применяются стандартные контрольные карты, даже при производстве мелких партий деталей (то есть при N между 30 и 100). Слежение за ходом производства по контрольным картам - естественное средство выяснения проблем. Однако невозможно определить, управляем ли станок статистически в течение длительного промежутка времени, если работать с краткосрочным планом выборки. Возникает вопрос: имеет ли исследование краткосрочной воспроизводимости какое-либо значение для предсказания долговременной работоспособности производства? Если предположить, что нестабильный процесс будет иметь большее стандартное отклонение, чем такой же стабильный, тог исследование потенциала краткосрочного процесса даст возможность определить круг проблем. Как правило, о процессе судят по оцененной воспроизводимости:

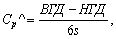(3)

где s - стандартное отклонение выборки, вычисленное для объема N.

К сожалению, кратковременному исследованию свойственны другие проблемы, такие, как тщательно подготовленные заготовки, новые инструменты, высококвалифицированные операторы и тому подобное, что может сделать сертификационный процесс отличным от типичных производственных операций. В общем, особые условия краткосрочного сертификационного исследования сокращают изменчивость относительно обычного производственного процесса. Таким образом, эти исследования в основном служат для выполнения более широкого круга проблем. Показатель C_p, рассчитанный на основе краткосрочного исследования, главным образом выявляет нижнюю границу изменчивости (потенциал процесса), которую можно ожидать на начальной стадии производства. Однако нет ничего невозможного в том, чтобы улучшить начальный C_p в результате дальнейшего совершенствования производства.

Обсуждение выборочных ситуаций

Выборочную вариацию C_p^ в (3) можно легко изучить, поскольку известно, как применить хи-квадрат распределение выборочной дисперсии (s²). Бурр (1976, pp. 336-341) выводит кривую оперативной характеристики (ОХ) для проверки стандартного отклонения, используя тот факт, что (N-l)s²/s ² имеет хи-квадрат распределение с (N-1) степенями свободы. По аналогии можно рассчитать кривую ОХ для проверки воспроизводимости процесса. Прежде всего следует отметить, что проверка гипотезы (s ₀>0)

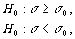
эквивалентна проверке воспроизводимости процесса (c₀>0)

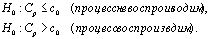(4)

При использовании критической области C_p^>с функция мощности критерия (4) получается непосредственно из хи-квадрат распределения выборочной дисперсии как:

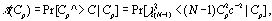(5)

где 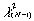- случайная величина с распределением хи-квадрат и с (N- 1) степенями свободы. Удобно брать функцию мощности для C_p, а не соответствующую функцию мощности для s , так как тогда не надо вводить поправку на различия в допусках процесса и “нормализованную” воспроизводимость процесса можно изучать непосредственно.

Пользуясь формулой (5), можно вычислить кривую ОХ (C_p)=1-p (C_p) и использовать ее для сравнения вариантов проверки. Кривая ОХ позволяет понять порочность практики, когда пренебрегают оценкой вариации выборки s ^ при оценивании воспроизводимости процесса. Пусть мы хотим выяснить, воспроизводим ли процесс на уровне C_o =1,33 (то есть H₀: C_p? 1,33) при N=30 изделиям, а предел браковки (критическое значение) c=1,33. Кривая ОХ (а) на рис. 4 показывает, что ОХ (1,33)=0,40, а это значит, что вероятность ложного суждения о процессе как о невоспроизводимом (принятие гипотезы H₀) равна 40%. Истинная воспроизводимость процесса должна быть C_p=1,6 чтобы оставалось всего 5% шансов для причисления процесса к невоспроизводимым при критическом значении С=1,33.

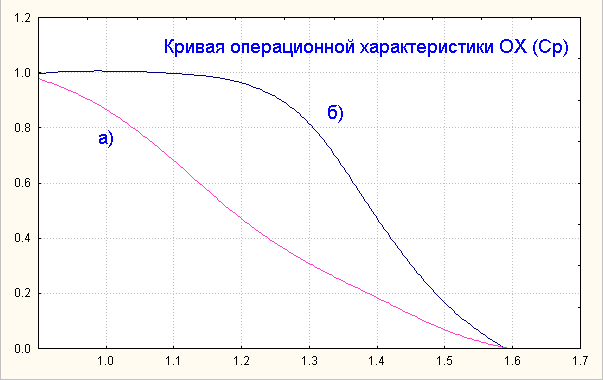
Рис.4.  Кривая оперативной характеристики для плана выборки, который отбрасывает гипотезу о воспроизводимости процесса, если Ср<c, где а) N=30, c=1.33 и б) N=70, c=1.46

Отбор разумного критического значения при проверке воспроизводимости требует назначения для значений С_p приемлемого уровня качества (AQL, ПУК) и неприемлемого уровня качества (RQL, НУК) (см. Бурр [1976, pp. 336-341]). Приемлемый уровень качества - это достаточно высокая воспроизводимость процесса, так что мы будем принимать процесс с воспроизводимостью выше, чем ПУК. НУК - это достаточно низкая воспроизводимость, так что мы отбросим процессы с воспроизводимостью ниже, чем НУК. Итак,

ПУК=C_p(высокая)>C_p(низкая)=НУК.

Исходя из формулы (5) a и b риски будут:

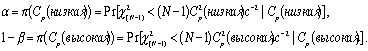
Решая относительно C_p(высокая)/C_p(низкая) и с получим:

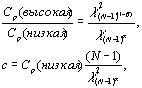
где 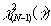- Хи (100-ый процентиль хи-квадрат распределения с (N-1) степенями свободы. В табл. 1 сведены значения для C_p(высокая)/C_p(низкая) и c/C_p(низкая) при разных объемах выборки и a =b равных 0,10 и 0,05. Критическое значение c и объем выборки N можно определить для любых конкретных значений C_p(высокой) и C_p(низкой). Например, если a =b =0,05, C_p(высокая)=1,6 и C_p(низкая)=1,2, то C_p(высокая)/C_p(низкая)=1,33, и из табл. 1: N=70 и c=(1,14)C_p(низкая)=1,37. Таким образом, беря критическое значение 1,37 и объем выборки 70, получаем вероятность 5% того, что процесс с C_p выше 1,6 будет признан невоспроизводимым (принята H₀), и что процесс с C_p ниже 1,2 будет признан воспроизводимым (отброшена H₀).

Чтобы гарантировать, что любой процесс с C_p ниже 1,33 (где ВГД-НГД=8s ) имеет высокую вероятность быть признанным невоспроизводимым (а = 0,1), а процесс с Ср выше 1,66 (где ВГД-НГД=10s ) имеет высокую вероятность быть признанным воспроизводимым (?=0,1), надо иметь C_p(высокая)/C_p(низкая)=1,25, и из табл. 1: N=70 и c/C_p(низкая)=1,10, что дает c=1,46. Кривая ОХ для такого рода плана выборки - кривая (б) на рис. 4.

Этот пример показывает, что практика использования N=30, имевшая место в прошлом в автомобильной промышленности для сертификации станков, в целом неадекватна. А практика использования минимального значения c=1,33, принятая в настоящее время, может характеризовать невыборочные проблемы, которые делают сертификационные испытания отличными от производства, но минимальное значение 1,33 не может адекватно учесть выборочную изменчивость. Возможно потребуются большее N и большее минимальное значение C_p. Шарбонно и Бебстер (1978, р. 112) предлагают для нового оборудования показатель воспроизводимости 1,5, не устанавливая, однако, объема выборки.

Подход с использованием интервала допуска

Альтернативный подход к определению работоспособности процесса - построение интервала длиной 2Ks такого, что 100p процентов результатов процесса покрывается данным интервалом с вероятностью g . Это стандартный подход к воспроизводимости процесса - метод интервала допуска. Интервалы допусков наряду с другими статистическими интервалами обсуждаются Ханом (1970). Можно доказать, что индекс C_p в формуле (4) допускает обобщение до:

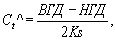(6)

где C_t^=C_p^, если К=3. Если мы выберем N=70, p=0,99, а g =0,95, то из табл. 2 интервал допуска имеет длину 6,042s, то есть в сущности тот же самый, что и при стандартном подходе. Однако для разных значений N, p и g будут разные интервалы. Например, при N=30 и техже самых значениях p и g , как и раньше, К=3,35, так что знаменатель в формуле (6) станет 6,7s. Таким образом, возрастающая неопределенность для N=30 отражается в росте сомножителя при s в знаменателе формулы (6).

Работоспособность процесса

Очевидно, что индекс C_p измеряет потенциал работоспособности процесса, так как только разброс процесса соотносится с границами допуска; положение среднего не учитывается. Можно получить любой процент бракованных деталей при высоком C_p просто при расположении среднего значения процесса достаточно близко к границе допуска. Таким образом, только потенциал работоспособности процесса количественно оценивается с помощью C_p, причем он достижим только для процессов, среднее которых совпадает с серединой между пределами допусков.

Показатель C_pk близок к индексу C_p, но использует среднее процесса и может рассматриваться как показатель его работоспособности. Есть две эквивалентные формы индекса C_pk. Первая формулировка получается при рассмотрении верхней и нижней границ допуска в отдельности. Вторая - использует отклонение среднего значения процесса от середины между пределами допусков. Приведем оба вывода, так как каждый из них по-разному освещает ситуацию.

Верхний и нижний показатели воспроизводимости

Рассмотрим ситуацию с односторонним допуском, когда задан только один предел. На рис. 5 показано распределение процесса относительно верхней границы допуска. Соотношение фактического и допустимого размаха точно так же, как и в (1), дает новый показатель CPU:

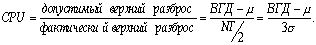(7)

Индекс CPU был разработан в Японии и применяется во многих японских компаниях. Для нижней границы допуска совершенно аналогично формуле (7) имеем:

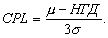
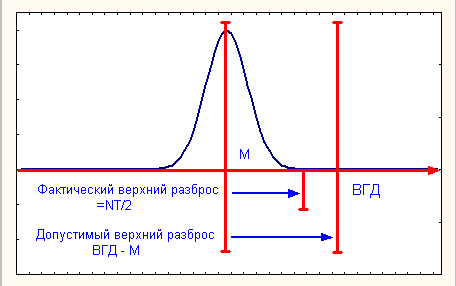
Рис.5. Соотношение параметров CPU

Оценки CPU и CPL обозначаются CPU и CPL и получаются при замене m и ? на ` х и s соответственно. Индексы CPU (верхний C_p) и CPL (нижний C_p) связаны с C_p через:

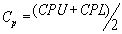
и применяются для измерения воспроизводимости процесса при наличии только одной границы допуска. Само собой разумеется, что в случае с одной границей допуска CPU=1,0 означает половину бракованных деталей (0,136%) по сравнению с тем, что дает C_p=1,0 в случае с двусторонним допуском.

Индекс C_pk. Так как CPU и CPL используют настройку процесса, естественный показатель для двусторонних допусков - это C_pk, где:

Cpk = Min {CPU, CPL} (8)

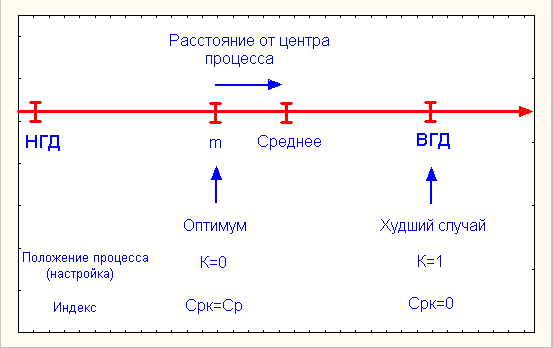
Рис.6. Соотношение параметров Срк

Таким образом, индекс C_pk использует нормированное расстояние между средним процесса и ближайшей границей допуска. Несколько другой подход - снижение величины C_p для процесса с помощью коэффициента (1-k), нормированного расстояния, на которое процесс удален от центра. Среднюю точку диапазона допуска находим по формуле:

m = (BГД + НГД) / 2.

Расстояние между средним значением процесса m , и оптимумом, средней точкой т, равно m -m, когда мы предполагаем, что т? m ? ВГД как показано на рис. 6. Нормированное расстояние равно:

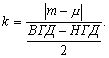(9)

Знак к абсолютному значению добавляется в том случае, когда НГД? m ? т. Оценка k обозначается через k^ и получается при замене m на ` x в формуле (9). Коэффициент k применяется в Японии как показатель, описывающий величину, на которую процесс смещен от центра. Индекс C_p, скорректированный на k в формуле (9) равен:

Cpk = Cp (1-k)  (10)

что алгебраически эквивалентно (8). Так как 0? k? 1, то C_pk? C_p, в предположении, что НГД? m ? ВГД.

Рассмотрим искусственный пример, пусть ВГД=20, НГД=8, s=2, ` х=16. Сначала заметим, что C_p=1,0, так что процесс потенциально воспроизводим, если настроен на среднюю точку m=14. Однако, CPL=1,33, CPU=0,67, k=0,33, что дает в результате C_pk=0,67. Приемлемый процесс потребует уменьшения s и/или центрирования m .

Номиналы (целевые значения)

Усилия по обеспечению качества изделий проходят четыре фазы. На первой фазе надо просто “делать деталь, как предписано”, причем проверка обычно используется для отбраковки по принципу “годно - не годно”, чтобы удостовериться, что все детали попали внутрь заданных на чертеже границ допуска. Вторая фаза - применение контрольных карт для установления стабильности процессов. Третья фаза - минимизация изменчивости для достижения однородности изделий. Идеи предупреждения дефектов (то есть предотвращение брака в процессе изготовления) и постоянное усовершенствование - часть этой фазы. Четвертая фаза - реализация улучшенной воспроизводимости процесса в более точной настройке средних на оптимальное значение показателя качества изделия или более традиционно – в минимизации затрат (то есть времени сборки). Последняя фаза не менее важна, чем предшествующие. Инженеры-разработчики концентрируются на вопросе “сколь многофункциональное изделие было бы лучше всего” вместо того, чтобы выяснить, сколько характеристик надо учитывать, чтобы изделие могло функционировать. Таким образом, инженеры-производственники должны теперь добиваться требуемого среднего (то есть целевого) значения, а также сохранять низкую изменчивость, чтобы процесс оставался между границами допуска.

Наиболее распространенное целевое значение, которое применяется на сегодняшний день, - середина между пределами допуска. Это значение часто выбирается как целевое (номинал) для снижения затрат, так как при этом минимизируется вероятность производства бракованного изделия. Сегодня эксцентричные номиналы чаще всего применяются для целенаправленного подбора размеров пар деталей, чтобы облегчить сборку, или для целевого подбора таких размерных цепей на операциях сборки, которые минимизировали бы трудности при проведении разборки. Джессуп (1983) рассматривает применение функции потерь Тагучи, которая ставит в соответствие отклонение от выбранного целевого значения и потери в деньгах. На рис. 7 показано соотношение целевого значения (Т), воспроизводимости процесса и затрат.

Рис.7. Воспроизводимость процесса в случае использования целевых значений (номиналов)

Есть множество способов распространения введенных показателей воспроизводимости на случай целевого значения (номинала). Следующее расширение использует аналогию между фактическим и допустимым разбросами процесса, которая показана на рис. 1. Показатель потенциала процесса связывает фактический разброс процесса с допустимым. Из рис. 8 для ближайшего к ВГД значения Т имеем:

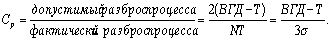
В общем:

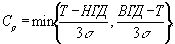(11)

Показатель C_p в формуле (11) - обобщение C_p из формулы (1), полученной из отношения допустимого разброса процесса к фактическому. При T=m показатели совпадают.

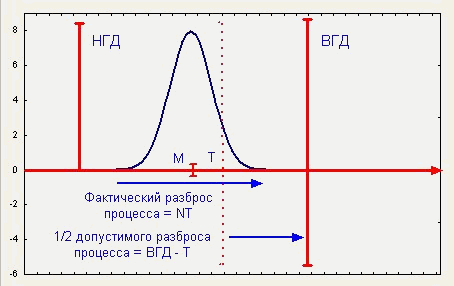
Рис.8. Соотношение параметров Ср при использовании целевых значений

Такую же аналогию можно применить и к показателю k. Из рис. 9 для ближайшего к ВГД значения T, имеем:

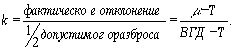
В общем:

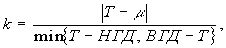(12)

где мы предполагаем, что m лежит внутри границ допуска и 0? k? 1. Показатель k в формуле (12) - обобщение показателя k из формулы (9), они эквивалентны при условии T=m . Таким образом индекс C_pk в формуле (10) может применяться при замене C_p и k соответственно на (11) и (12):

Cpk =Min {CPU, CPL}.

где

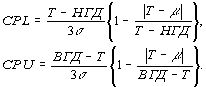
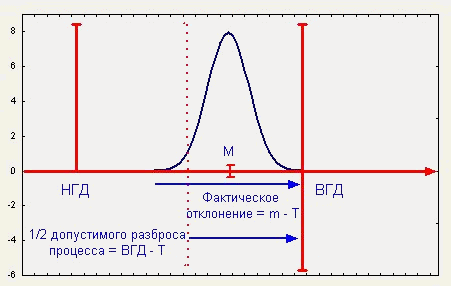
Рис.9. Соотношение параметров К при использовании целевых значений

Обратите внимание, что СPL=0, если |Т-m |>T-НГД, и CPU=0, если |Т-m |>ВГД-T. Эти показатели можно использовать при односторонней границе допуска с целевым значением. Вышеприведенные уравнения аналогичны (8) для C_pk и соответственно CPL и CPU, при условии, что Т=m .

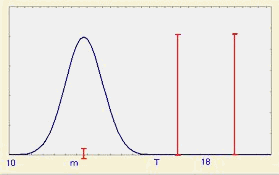
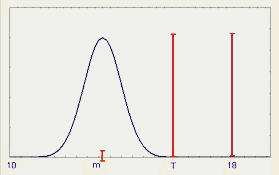
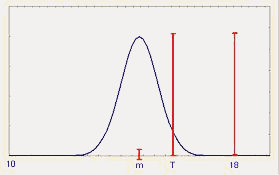
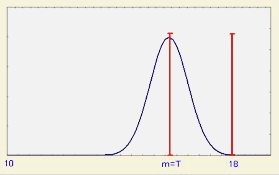
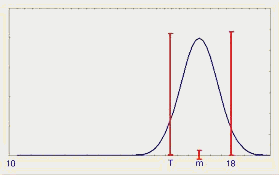
Простой пример иллюстрирует применение этих индексов. Предположим, что ВГД=18, НГД=10, T=16, s =0,67. Обратите внимание, что из формулы (11) C_p=1,0. На рис. 10 представлены индексы воспроизводимости для выбранных значений среднего.

Распределение	m	CPL	CPU	k	Cpk
	13	15	00	10	00
	14	20	00	10	00
	15	25	05	05	05
	16	30	10	00	10
	17	25	05	05	05

Рис.10.  Индексы воспроизводимости процесса при целевом значении T=16

Заметьте, что из-за того, что C_pk скорректировано на отклонении от Т, может быть воспроизводимость 0 и не быть ни одной детали за пределами допуска. Таким образом, отклонения в “длинную сторону” (то есть, туда, где расстояние между Т и границей допуска максимально) от целевого значения Т влечет за собой такое же уменьшение C_pk, что и отклонение в “короткую сторону” (то есть туда, где расстояние между Т и границей допуска минимально).

Недостатки

Опыт показал, что в использовании C_p и C_pk на традиционной основе заложены потенциальные трудности. Эти недостатки в общем возникают из-за пользователей, которые не имеют полного представления о статистических принципах, а не из-за проблем, присущих самим индексам. Некоторые из этих недостатков описываются ниже.

(1) Статистическая управляемость - Существует тенденция к определению воспроизводимости процесса до того, как сам процесс войдет в состояние статистической управляемости. Воспроизводимость количественно характеризует обычную вариацию и показывает, что можно ожидать от процесса в будущем. Наличие конкретных причин вариации делает предсказания невозможными, а смысл воспроизводимости неясным.

(2) План выборки - Очевидно, что значения среднего размаха ` R, часто используемого для оценки s , зависит от плана выборки. Таким образом, можно доказать, что значение показателя воспроизводимости можно легко менять простым изменением плана выборки. Ситуация покажется еще более сложной, если учесть замечание, которое сделал У. Эдвардс Деминг инженеру, говорившему о своих достижениях при введении процесса в состояние статистической управляемости. Деминг заявил, что он мог бы любой процесс ввести в это состояние, причем просто для выборки внутри подгрупп во времени. Это утверждение следует из признания того факта, что число источников вариации растет с увеличением интервала времени между выборками внутри подгруппы. Рассеивание выборок внутри подгрупп во времени будет увеличивать ` R, расширяя контрольные пределы и, следовательно, делая достижение статистически управляемого состояния более вероятным. Однако увеличение ` R будет увеличивать и оценку s , а значит уменьшать воспроизводимость процесса. И наоборот: можно увеличить воспроизводимость процесса, используя выборки последовательных деталей (то есть получая малый размах ` R), чтобы получить минимум оценки s и максимум воспроизводимости. Однако в этом случае труднее всего добиться статистической управляемости, так как расстояние между контрольными пределами может стать наименьшим. Таким образом, рассмотрение только статистической управляемости или только воспроизводимости процесса в отдельности не даст устойчивой оценки работоспособности процесса - оба критерия надо рассматривать совместно.

(3) Вычисления - Иногда бывает трудно вычислять C_p и C_pk непосредственно в цехе, где не все люди привыкли к математическим формулам. Эту проблему можно рассматривать по-разному, но часто она требует определенного обучения и (или) некоторой автоматизации.

(4) Ненормальность - Изменчивость результатов процесса может быть следствием ненормального распределения показателя. Вероятно, есть смысл ожидать, что индексы воспроизводимости в некоторой степени чувствительны к отклонениям от нормальности. Для получения приближенной нормальности могут пригодиться преобразования данных. Итак, можно определить процент бракованных деталей как непосредственно, так и подобрав распределение. Этот процент можно привести к эквивалентному индексу воспроизводимости для процесса, имеющего нормальное распределение.

(5) Износ инструмента - В ситуации, когда изнашивается инструмент, первичный интерес представляет оценка ` R по последовательному плану выборки. Технически ` R можно применять для оценки C_p, но воспроизводимость обычно довольно высока. Работоспособность процесса зависит от частоты смены инструмента. Это делает неудобным распространение показателя C_pk в такой ситуации.

Применения

Цель любого индекса - удобная свертка информации в наиболее подходящей форме. Статистики ` х и s содержат большую часть информации о предполагаемом нормальном процессе и самыми разными способами могут быть соотнесены с ВГД и НГД. Пять показателей воспроизводимости C_p, CPU, CPL, k и C_pk, приведенных в табл. 2, составляют специальный “язык”, который понятен как в цехе, так и в конторе управляющего. Некоторые области применения описываются ниже, но в любом конкретном приложении индексов надо учитывать описанные выше недостатки.

Показатель	Уравнение оценивания	Применение
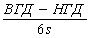
Ср		Потенциал процесса для двусторонних границ допуска
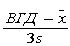
CPU		Работоспособность процесса относительно верхней границы допуска
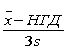
CPL		Работоспособность процесса относительно нижней границы допуска
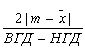
k		Отклонение среднего значения процесса от середины (m) между границами допуска
Cpk	Min {CPL, CPU} = Cp (1-k)	Работоспособность процесса для двусторонних границ допуска

Таблица 2. Показатели воспроизводимости Сp, СPU, CPL, k Cpk

(1) Предупреждение бракованной продукции- для различных типов испытаний станков и сертификации процессов иногда бывает полезно и целесообразно установить норму воспроизводимости. Типичная норма воспроизводимости - это C_pk=l,33, что делает появление брака маловероятным (см. Хоффнер, 1985) во многих ситуациях. Обратите внимание: так как воспроизводимость обычно уже оценена, надо брать более высокое критическое значение (с), чем предлагалось ранее.

(2) Непрерывное совершенствование - Внутри отдела или цеха часто бывает полезно непрерывно следить за совершенствованием, что можно осуществить, наблюдая за изменяющимися распределениями воспроизводимостей процесса. Если, например, было 10% процессов с воспроизводимостями между 1 и 1,33 в данном месяце, а в следующем месяце некоторые из них имеют этот показатель между 1,33 и 1,67, то усовершенствование произошло. За таким сдвигом распределений легко осуществить мониторинг.

(3) Коммуникация - Применение C_p и C_pk образует общий язык, который не зависит от конкретных размеров и оценивает как потенциальную, так и фактическую работоспособность производственных процессов. Инженеры-разработчики и производственники получают возможность общения друг с другом и выявления процессов с высокой воспроизводимостью. Изменения в проекте могут способствовать сокращению затрат. Производственники могут непосредственно общаться с поставщиками (см., например, Сулливан, 1984).

(4) Установление приоритетов - Простая компьютерная распечатка процессов с неприемлемыми значениями C_p или C_pk - помощница в установлении приоритетов совершенствования процессов.

(5) Настройка или изменчивость - Для любого показателя всегда имеет смысл сравнить C_p и C_pk. Если C_pk слишком мало, то надо выяснить для C_p, не слишком ли велика изменчивость. Если C_p близко к C_pk, то с настройкой процесса нет проблем. Индексы CPU, CPL и k показывают, насколько близко среднее подошло к границам допуска и насколько далеко оно от целевого значения.

(6) Проверки - Для оценки работоспособности систем применяются различные типы проверок качества. Сравнение воспроизводимостей внутренних с воспроизводимостями, определенными в результате проверки, может помочь выделить области, где возникают проблемы.

Выводы

Показатели воспроизводимости могут применяться для эффективной свертки информации о процессе удобным способом. Индексы C_p, CPU, CPL, k и C_pk образуют группу взаимодополняющих показателей, которые образуют удобную безразмерную систему. Все эти показатели вместе определяют, имеет ли процесс достаточно низкую изменчивость и удовлетворяет допускам процесса или есть проблема настройки. Они могут применяться для односторонних и двусторонних пределов допуска и могут обобщаться для работы с многомерными номиналами (показателями качества).Вероятно, наибольшая ценность этих показателей - в поддержке усилий, направленных на предотвращение производства брака, а также в том, что дает метод мониторинга и непрерывного совершенствования в широком диапазоне. Наконец, эти показатели позволяют установить эффективный обмен информацией о потенциале процесса и его работоспособности на языке, который легко понимать.

Литература

Burr, 1. R. (1976). Statistical Quality Control Methods Marcel Dekker, New York, New York. ;

Charbonneau, H. C. and Webster, G. L. (1978). Industrial Quality Control. Prentice Hall, Englewood Cliffs, New Jersey.

Ford Motor Company (1984). Continuing Process Control and Process Capability lpmrovement. Ford Motor Company, Dearborn, MI.

Hahn, G. J. (1970). „Statistical Intervals for a Normal Population Part 1. Tables. Examples and Applications." Journal of Quality Technology 2, pp. 115-125.

Hotter, P. (1985). „Moving to Prevention: An Industry in Transition." Quality Progress 18, pp. 24-26.

Jessup, P. T. (1983). „Process Capability, The Value of Improved Performance," paper presented at the ASQC Automotive Division Workshop Seminar, November 2-4, Southfield, Michigan.

Juran, J. M. and Gryna, F. M. (1980). Quality Planning and Analysis McGraw-Hill, New York, New York.

Juran, J. M. Gryna, F. M., and Bingham, R. S. (1979). Quality Control Handbook. McGraw-Hill, New York, New York.

Sullivan, L. P. (1984). „Reducing Variability: A New Approach to Quality." Quality Progress 17, pp. 16-21

Sullivan, L. P. (1985). „Letters." Quality Progress 18, pp. 7-8. Key Words: Capability, Target Value, Process Potential Process Performance.